
����Ŀ����֪������y=��![]() x2+
x2+![]() x+4��x���ڵ�A��B����y���ڵ�C������AC��BC��
x+4��x���ڵ�A��B����y���ڵ�C������AC��BC��
��1����A��B�������Լ�ֱ��BC�Ľ���ʽ��
��2����ͼ1������P�ӵ�B������ÿ��5����λ���ٶ����O�˶�������P��y���ƽ���߽��߶�BC�ڵ�M�����������ڵ�N������N��NC��BC��BC�ڵ�K������MNK����MPB�������Ϊ1��2ʱ����P���˶�ʱ��t��ֵ��
��3����ͼ2������P �ӵ�B������ÿ��5����λ���ٶ����A�˶���ͬʱ��һ������Q�ӵ�A������AC����ͬ�ٶ����յ�C�˶�����P��Qͬʱֹͣ���ֱ���PQ��BPΪ����x���Ϸ���������PQEF��������BPGH�������ζ��㰴˳ʱ��˳����������PQEF��������BPGH�ص�������һ����Գ�ͼ��ʱ���������ʱ��Գ�ͼ�ε������

���𰸡���1��y=��x+4��2��PB=1��t=![]() ��3����
��3����![]() ��
��![]()
�������������������1����y=0���ⷽ����![]() x2+
x2+![]() x+4=0���������A��B���꣬�����ô���ϵ�������ֱ��BC��
x+4=0���������A��B���꣬�����ô���ϵ�������ֱ��BC��
��2����ͼ1�У���P��a��0����ֻҪ֤��MN=PB���г����̼��ɽ�����⣮
��3������ͼ2�У�����Գ�ͼ��Ϊ����ʱ���г���������˶�ʱ�伴�ɣ�����ͼ3�У�����Գ�ͼ����������ʱ���г��������ʱ�伴�ɣ�
�����������1����y=0������![]() x2+
x2+![]() x+4=0�����x=4����3��
x+4=0�����x=4����3��
����A���꣨��3��0������B���꣨4��0����
��ֱ��BC����ʽΪy=kx+b����B��4��0����C��0��4������
��![]() �����
�����![]() ��
��
��ֱ��BC����ʽΪy=��x+4��
��2����ͼ1�У���PN��OC��NK��BC��
���MPB=��MKN=90����
�ߡ�PMB=��NMK��
���MNK�ס�MPB��
�ߡ�MNK����MPB�������Ϊ1��2��
��BM=![]() MN��
MN��
��OB=OC��
���PBM=45����
��BM=P![]() B��
B��
��MN=PB����P��a��0������MN=��![]() a2+
a2+![]() a+4+a��4=��
a+4+a��4=��![]() a2+
a2+![]() a��BP=4��a��
a��BP=4��a��
����![]() a2+
a2+![]() a=4��a��
a=4��a��
���a=3��4����������
��PB=1��t=![]() ��
��

��3����ͼ2�У�����Գ�ͼ��Ϊ����ʱ��PF=PG��GM=FM��

��BP=PG=AQ��PQ=PF��
��AQ=PQ=5t��
����Q��QN��AP����AN=NP������AQN�ס�ACQ��
��![]() ��
��
��![]() ��
��
��AN=3t��
��AP=2AN=6t��
��AP+BP=AB��
��5t+6t=7��
��t=![]() ��
��
��PB=PF=![]() ��
��
����ACO�ס�FPR�ס�MFT��
��![]() ��
��
��FR=![]() ��TF=
��TF=![]() ��
��
��![]() ��
��
��FM=![]() ��
��
��S=2��![]() ��PF��FM=
��PF��FM=![]() ��
��
����ͼ3�У�����Գ�ͼ����������ʱ��
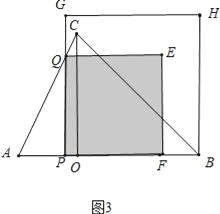
3t+5t=7��
��t=![]() ��
��
��S=![]() ��
��


 �����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���籾��ͼ�٣��ڡ�ABC�У���֪��ABC=��ACB=��������A��BC��ƽ�������ABC��ƽ���߽��ڵ�D������CD��
��1�����ACD�Ĵ�С��
��2�����߶�CD���ӳ�����ȡһ��F����FDΪ�ǵ�һ������DFE=������һ�߽�BD�ӳ����ڵ�E����FD=kAD���籾��ͼ����ʾ��������![]() ��ֵ���ú�k�Ĵ���ʽ��ʾ����
��ֵ���ú�k�Ĵ���ʽ��ʾ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�Ա�������ĺ�����ϵ��ͼ��������3����ͬ�������龳��
��С���ﳵ��400��/�ֵ��ٶ���������5�֣���ԭ����Ϣ��4�֣�Ȼ����500��/�ֵ��ٶ�������س����أ���ʱ��Ϊx�֣�������صľ���Ϊyǧ�ף�
����һ���ݻ�Ϊ6���Ŀ��ڿ�Ͱ��С����1.2��/�ֵ��ٶ������������Ͱעˮ��ע5�ֺ�ֹͣ����4�ֺ�����2��/�ֵ��ٶ����ٵ���Ͱ�е�ˮ����ʱ��Ϊx�֣�Ͱ�ڵ�ˮ��Ϊy����
������ABCD�У�AB=4��BC=3������P�ӵ�A�����������ضԽ���AC����CD����DA�˶�����Aֹͣ�����P���˶�·��Ϊx������P���A���غ�ʱ��y=S��ABP������P���A�غ�ʱ��y=0��
���У�����ͼ����ʾ������ϵ�������龳�ĸ���Ϊ
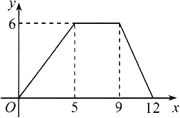
A��0 B��1 C��2 D��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OΪABCD�ĶԽ���AC���е㣬����O��һ��ֱ�߷ֱ���AB��CD���ڵ�M��N����E��F��ֱ��MN�ϣ���OE��OF.
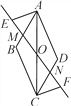
(1)ͼ�й��м���ȫ�������Σ�������Ƕ�д������
(2)��֤����MAE����NCF.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������2[��m��1��m+m��m+1��][��m��1��m��m��m+1��]����m��������������۲컯���Ľ�����㷢��ԭʽ��ʾһ��ʲô����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y1=![]() 2+bx+c��x�ύ�ڵ�A��B����y���ڵ�C��0����2
2+bx+c��x�ύ�ڵ�A��B����y���ڵ�C��0����2![]() �����������߶Գ���x=��2��x���ڵ�D��E���������ڵ�3������һ���㣮
�����������߶Գ���x=��2��x���ڵ�D��E���������ڵ�3������һ���㣮
��1����������y1�Ľ���ʽ��
��2������OCD��CD���ۺ�O��ԳƵ�O���Ƿ���������y1�ϣ���˵�����ɣ�
��3������E����ֱ��CD�ĶԳƵ�E��ǡ������x���ϣ���E����x��Ĵ��߽�������y1�ڵ�F�������F�����ꣻ��ֱ��CD���Ƿ���ڵ�P��ʹ|PE��PF|��������ڣ���д��|PE��PF|���ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���y=kx+b��k��0����ͼ����x�ᡢy��ֱ���A��B���㣬���뷴��������y=![]() ��m��0����ͼ���ڵ�һ�����ڵ�C��CD��ֱ��x�ᣬ����ΪD����OA=OB=OD=1��
��m��0����ͼ���ڵ�һ�����ڵ�C��CD��ֱ��x�ᣬ����ΪD����OA=OB=OD=1��
��1�����A��B��D�����ꣻ
��2����һ�κ����뷴���������Ľ���ʽ��
��3����x��0�������£�����ͼ��˵��������������ֵ����һ�κ���ֵ��x��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A=90�㣬AB=4��AC=3��M��AB�ϵĶ��㣨����A��B�غϣ�����M����MN��BC��AC�ڵ�N��
��1����ͼ1���ѡ�AMN��ֱ��MN�۵��õ���PMN����AM=x��
i������P�����ڱ�BC�ϣ���x��ֵ��
ii����M���˶������У��ǡ�MNP������BCNM�غϵ����Ϊy������y����x�ĺ�����ϵʽ������y�����ֵ��
��2����ͼ2����MNΪֱ������O�����ڡ�O�����ڽӾ���AMQN�����ж�ֱ��BC���O��λ�ù�ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com