
【题目】如图,D,E,F,G,H,I是三角形ABC三边上的点,连结EI,EF∥BC, GH∥AC, DI∥AB.

(1)写出与∠IEC是同旁内角的角。
(2)判断∠GHC与∠FEC是否相等,并说明理由。
(3)若EI平分∠FEC,∠C=56°,∠B=50°,求∠EID的度数。
【答案】(1)与∠IEC是同旁内角的角是:∠C、∠EDI、∠EIC、∠EID ,(2)∠GHC=∠FEC ,理由见解析,(3)12°.
【解析】
试题分析:(1)根据同旁内角的定义确定即可;(2)利用平行线的性质得出∠FEC+∠C=180°和∠GHC+∠C=180°,再利用补角的性质即可得出结论;(3)利用平行线的性质得出∠FEC=180°-∠C=124°,∠DIC=∠B=50°,利用角的平分线得出∠FEI=![]() ∠FEC=62°,然后利用角的和差关系即可得出结论.
∠FEC=62°,然后利用角的和差关系即可得出结论.
试题解析:(1)与∠IEC是同旁内角的角是:∠C、∠EDI、∠EIC、∠EID
(2)∠GHC=∠FEC
理由:∵EF∥BC
∴∠FEC+∠C=180°
∵GH∥AC
∴∠GHC+∠C=180°
∴∠GHC=∠FEC
(3) ∵EF∥BC,∠C=56°
∴∠FEC+∠C=180°
∴∠FEC=180°-∠C=124°
∵EI平分∠FEC
∴∠FEI=![]() ∠FEC=62°
∠FEC=62°
∴∠FEI=∠EIC=62°
∵DI∥AB,∠B=50°
∴∠DIC=∠B=50°
∴∠EID=∠EIC-∠DIC=12°


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,射线OA∥射线CB,∠C=∠OAB=100°.点D、E在线段CB上,且∠DOB=∠BOA, OE平分∠DOC.
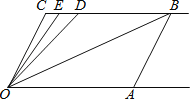
(1)试说明AB∥OC的理由;
(2)试求∠BOE的度数;
(3)平移线段AB;
①试问∠OBC:∠ODC的值是否会发生变化?若不会,请求出这个比值;若会,请找出相应变化规律.
②若在平移过程中存在某种情况使得∠OEC=∠OBA,试求此时∠OEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与X轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:
①4a﹣2b+c<0;②2a﹣b<0;③a+c<1;④b2+8a>4ac,
其中正确的有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=﹣x2+x+2,则当y<0时,自变量x的取值范围是( )
A.x<﹣1或x>2 B.﹣1<x<2
C.x<﹣2或x>1 D.﹣2<x<1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.“打开电视机,正在播放《动物世界》”是必然事件
B.某种彩票的中奖概率为![]() ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖
C.抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为![]()
D.想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(﹣3,2).请按要求分别完成下列各小题:
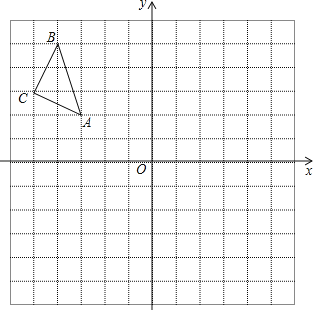
(1)把△ABC向下平移4个单位得到△A1B1C1,画出△A1B1C1,点A1的坐标是 ;
(2)画出△ABC关于y轴对称的△A2B2C2;点C2的坐标是 ;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线y=3x+3与x轴交于C点,与y轴交于A点,B点在x轴上,△OAB是等腰直角三角形.

(1)求过A、B、C三点的抛物线的解析式;
(2)若直线CD∥AB交抛物线于D点,求D点的坐标;
(3)若P点是抛物线上的动点,且在第一象限,那么△PAB是否有最大面积?若有,求出此时P点的坐标和△PAB的最大面积;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com