
 ��ͼ����֪���κ���y=m2x2-2mx-3��m�dz�����m��0����ͼ����x��ֱ��ཻ�ڵ�A��B����Aλ�ڵ�B����ࣩ����y�ύ�ڵ�C���Գ���Ϊֱ��l����C����l�ĶԳƵ�ΪD������AD����EΪ�ú���ͼ����һ�㣬ABƽ�֡�DAE��
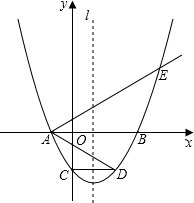
��ͼ����֪���κ���y=m2x2-2mx-3��m�dz�����m��0����ͼ����x��ֱ��ཻ�ڵ�A��B����Aλ�ڵ�B����ࣩ����y�ύ�ڵ�C���Գ���Ϊֱ��l����C����l�ĶԳƵ�ΪD������AD����EΪ�ú���ͼ����һ�㣬ABƽ�֡�DAE������ ��1������y=0�������������x��Ľ������ꣻ
�ڸ��������߽���ʽȷ�����Գ��ᣬ��y�ύ�����ꣻ
��2�������M������꣬������������㣬���þ��εĶԽ�����ƽ����ȷ������M�����꣬���ù��ɶ������㼴�ɣ�
��� �⣺��1������y=0����mx-3����mx+1��=0��
��x=-$\frac{1}{m}$��x=$\frac{3}{m}$��
��A��-$\frac{1}{m}$��0����B��$\frac{3}{m}$��0����
��AB=$\frac{4}{m}$��
�ʴ�Ϊ$\frac{4}{m}$��
�ڡ߶��κ���y=m2x2-2mx-3��
��C��0��-3�����Գ���l��x=$\frac{1}{m}$��
��D��$\frac{2}{m}$��-3��
��ABƽ�֡�DAE��
���D����x��ĶԳƵ�Q��$\frac{2}{m}$��3����ֱ��AE�ϣ�
��ֱ��AE�Ľ���ʽΪy=mx+1��
�ߵ�E�������ߺ�ֱ��AE�Ľ��㣬
��E��$\frac{4}{m}$��5����
��2����M��x��m2x2-2mx-3����N��$\frac{1}{m}$��a��
��A��-$\frac{1}{m}$��0����E��$\frac{4}{m}$��5����
��A��E��M��NΪ������ı����Ǿ��Σ�
����AE��MNΪ�Խ���ʱ��
AE��MN���е��غϣ�
��-$\frac{1}{m}$+$\frac{4}{m}$=x+$\frac{1}{m}$��
��x=$\frac{2}{m}$��
��M��$\frac{2}{m}$��-3����
��MA2+ME2=AE2��
��$\frac{9}{{m}^{2}}$+9+$\frac{4}{{m}^{2}}$+64=$\frac{25}{{m}^{2}}$+25��
��m=-$\frac{1}{2}$���ᣩ����m=$\frac{1}{2}$��
��M��4��-3����
����AN��MEΪ�Խ���ʱ��
AN��ME���е��غϣ�
��-$\frac{1}{m}$+$\frac{1}{m}$=x+$\frac{4}{m}$��
��x=-$\frac{4}{m}$��
��M��-$\frac{4}{m}$��21����
��AE2+AM2=ME2��
��$\frac{25}{{m}^{2}}$+25+$\frac{9}{{m}^{2}}$+441=$\frac{64}{{m}^{2}}$+256��
��m=-$\frac{1}{\sqrt{7}}$���ᣩ��m=$\frac{1}{\sqrt{7}}$
��$M��-4\sqrt{7}��21��$��
����AM��NEΪ�Խ���ʱ��
��AM��NE���е��غϣ�
��x+��-$\frac{1}{m}$��=$\frac{1}{m}$+$\frac{4}{m}$��
��x=$\frac{6}{m}$��
��M��$\frac{6}{m}$��21����
��AE2+EM2=AM2��
��$\frac{25}{{m}^{2}}$+25+$\frac{4}{{m}^{2}}$+256=$\frac{49}{{m}^{2}}$+441���˷����⣬
�������ڣ�M��4��-3����$M��-4\sqrt{7}��21��$��
���� �����Ƕ��κ����ۺ��⣬��Ҫ��������������������Ľ������꣬�Գ��ᣬ���ɶ��������ε����ʣ��Ȿ��Ĺؼ����ý�ƽ���ߵõ�ֱ��AB����ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
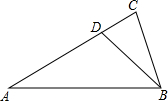 ��ͼ����A=��CBD=30�㣬��ABD=45�㣬�����½��۴�����ǣ�������
��ͼ����A=��CBD=30�㣬��ABD=45�㣬�����½��۴�����ǣ�������| A�� | AB=3CD | B�� | BC2=CD•AB | ||
| C�� | ��BCD�ǵ��������� | D�� | 2CD=��$\sqrt{3}-1$��AD |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a-1=-a | B�� | a0=1 | C�� | ��-a��2=-a2 | D�� | ��-ab��3=-ab3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����ε������ߺ����ǵļн� | B�� | �����ε������� | ||
| C�� | �����ε������Ǻ����ǵļб� | D�� | �����ε������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
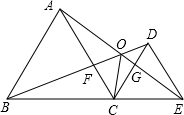 ��ͼ����֪��ABC�͡�DCE���ǵȱ������Σ���B��C��E��ͬһ��ֱ���ϣ�AE��BD���ڵ�O��AE��CD���ڵ�G��AC��BD���ڵ�F������OC��FG�������н��ۣ���AE=BD����AG=BF����FG=CG���ܡ�BOC=��EOC����FG��BE�����н�����ȷ���Ǣ٢ڢۢܢݣ�ֻ����ţ�
��ͼ����֪��ABC�͡�DCE���ǵȱ������Σ���B��C��E��ͬһ��ֱ���ϣ�AE��BD���ڵ�O��AE��CD���ڵ�G��AC��BD���ڵ�F������OC��FG�������н��ۣ���AE=BD����AG=BF����FG=CG���ܡ�BOC=��EOC����FG��BE�����н�����ȷ���Ǣ٢ڢۢܢݣ�ֻ����ţ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����������һ��·�ڣ�������� | |
| B�� | 400���������˵�������ͬһ�� | |
| C�� | �����߶ο������һ�������� | |
| D�� | ������һ�ŵ�ӰƱ����λ����2�ı��� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com