
【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O,BD=6cm,AD=8cm,AB=10cm,点E从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,点G从点C出发,沿CB方向匀速运动,速度为2cm/s;当一个点停止运动时,另一个点也停止运动.连接OE,过点G作GF∥BD,设运动时间为t(s)(0<t<4),解答下列问题:
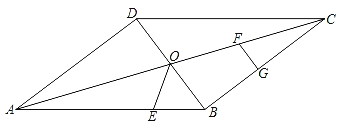
(1)当t为何值时,△BOE是等腰三角形?
(2)设五边形OEBGF面积为S,试确定S与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使S五边形OEBGF:S△ACD=19:40?若存在,求出t的值;若不存在,请说明理由;
(4)在运动过程中,是否存在某一时刻t,使得OB平分∠COE,若存在,求出t的值;若不存在,请说明理由.
【答案】(1)t为3或![]() 或
或![]() 秒;(2)S五边形BEOFG=﹣
秒;(2)S五边形BEOFG=﹣![]() t+12;(3)2秒;(4)存在t为
t+12;(3)2秒;(4)存在t为![]() 秒时,使OB平分∠COE
秒时,使OB平分∠COE
【解析】
(1)证出△ADB为直角三角形,且∠ADB=90°,分以下三种情况讨论,①当BO=BE时,可得出t=3,②当BO=EO时,如图1,过点O作OH⊥BE于点H,证明△BOH∽△BAD,可得出答案;③当BE=OE,如图2,过点E作EK⊥OB于点K,证明△BEK∽△BAD,由比例线段可得出答案;
(2)证明△CFG∽△COB,求出S△CFG=![]() ,根据S五边形BEOFG=S△BOE+S四边形BOFG可得出答案;
,根据S五边形BEOFG=S△BOE+S四边形BOFG可得出答案;
(3)由(2)的结论可得出t的方程,解方程即可得解;
(4)证明△EOK∽△COB,可得出![]() ,则可得解.
,则可得解.
(1)在△ADB中,
∵AD2+BD2=82+62=100=AB2,
∴△ADB为直角三角形,且∠ADB=90°,
若△BOE为等腰三角形,分以下三种情况讨论,
①当BO=BE时,
t=3,
②当BO=EO时,如图1,过点O作OH⊥BE于点H,
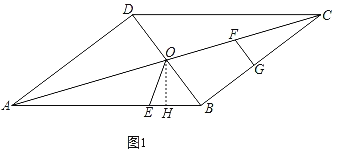
∵∠ABD=∠ABD,∠OHB=∠ADB=90°,
∴△BOH∽△BAD,
∴![]() ,
,
即![]() ,
,
则BH=![]() ,OH=
,OH=![]() ,
,
∵OE=OB,OH⊥BE,
∴BH=![]() BE,
BE,
即![]() ,
,
∴t=![]() ,
,
③当BE=OE,如图2,
过点E作EK⊥OB于点K,
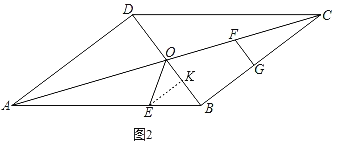
∵∠ABD=∠ABD,∠BKE=∠ADB=90°,
∴△BEK∽△BAD,
∴![]() ,
,
即![]() ,
,
∴BK=![]() t,EK=
t,EK=![]() t,
t,
∵OE=EB,EK⊥BO,
∴BK=![]() BO,
BO,
即![]() ,
,
∴t=![]() ,
,
答:当t为3或![]() 或
或![]() 秒时,△BOE是等腰三角形;
秒时,△BOE是等腰三角形;
(2)∵GF∥BD,
∴∠CFG=∠COB,∠CGF=∠CBO,
∴△CFG∽△COB,
∴![]() ,
,
∴S△CFG=![]() ,
,
∴S四边形BOFG=S△BOC﹣S△CFG=12﹣![]() ,
,
∵S△BOE=![]() BE×OH=
BE×OH=![]() ,
,
∴S五边形BEOFG=S△BOE+S四边形BOFG=12﹣![]() =﹣
=﹣![]() t+12,
t+12,
(3)若S五边形OEBGF:S△ACD=19:40,
∴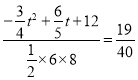 ,
,
整理得:5t2﹣8t﹣4=0,
解得:t1=![]() (舍去),t2=2.
(舍去),t2=2.
答:存在t为2秒时,使S五边形OEBGF:S△ACD=19:40;
(4)若OB平分∠COE,
则∠BOE=∠BOC,∠EKO=∠CBO=90°,
∴△EOK∽△COB,
∴![]() ,
,
∴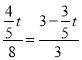 ,
,
解得:t=![]() .
.
答:存在t为![]() 秒时,使OB平分∠COE.
秒时,使OB平分∠COE.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】某电器商场销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是该型号电风扇近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
![]() 求A、B两种型号的电风扇的销售单价;
求A、B两种型号的电风扇的销售单价;
![]() 若该商场准备用不多于5400元的金额再采购这两种型号的电风扇共30台,假设售价不变,那么商场应采用哪种采购方案,才能使得当销售完这些风扇后,商场获利最多?最多可获利多少元?
若该商场准备用不多于5400元的金额再采购这两种型号的电风扇共30台,假设售价不变,那么商场应采用哪种采购方案,才能使得当销售完这些风扇后,商场获利最多?最多可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)
借助图形的直观性,我们可以直接得到一些有规律的算式的结果,比如:由图①,通过对小黑点的计数,我们可以得到1+2+3+…+n=![]() n(n+1);由图②,通过对小圆圈的计数,我们可以得到1+3+5+…+(2n﹣1)=n2.
n(n+1);由图②,通过对小圆圈的计数,我们可以得到1+3+5+…+(2n﹣1)=n2.

那么13+23+33+…+n3结果等于多少呢?
如图③,AB是正方形ABCD的一边,BB′=n,B′B″=n﹣1,B″B′′′=n﹣2,……,显然AB=1+2+3+…+n=![]() n(n+1),分别以AB′、AB″、AB′′′、…为边作正方形,将正方形ABCD分割成块,面积分别记为Sn、Sn﹣1、Sn﹣2、…、S1.
n(n+1),分别以AB′、AB″、AB′′′、…为边作正方形,将正方形ABCD分割成块,面积分别记为Sn、Sn﹣1、Sn﹣2、…、S1.
(规律探究)
结合图形,可以得到Sn=2BB′×BC﹣BB′2= ,
同理有Sn﹣1= ,Sn﹣2= ,…,S1=13.
所以13+23+33+…+n3=S四边形ABCD= .
(解决问题)
根据以上发现,计算![]() 的结果为 .
的结果为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费悄况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调査,根据调查结果绘制成两幅不完整的统计图表.
请你根据统计图表提供的信息,解答下列问题:
组別 | 家庭年文化教育消费金额x(元) | 户数 |
A | x≤5000 | 36 |
B | 5000<x≤10000 | m |
C | 10000<x≤15000 | 27 |
D | 15000<x≤20000 | 15 |
E | x>20000 | 30 |
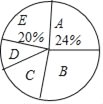
(1)本次被调査的家庭有__________户,表中 m=__________;
(2)本次调查数据的中位数出现在__________组.扇形统计图中,D组所在扇形的圆心角是__________度;
(3)这个社区有2500户家庭,请你估计家庭年文化教育消费10000元以上的家庭有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,点E在AD边上,连接BE、CE,EB平分∠AEC .
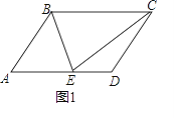
(1)如图1,判断△BCE的形状,并说明理由;
(2)如图2,若∠A=90°,BC=5,AE=1,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、点D为⊙O上两点,线段BC切⊙O于点B,点D在BC的垂直平分线上,CD∥OA,sin∠BCD=![]() ,OA=2BD,若BC=
,OA=2BD,若BC=![]() ,则⊙O的半径为( )
,则⊙O的半径为( )
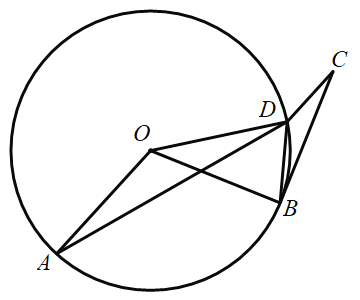
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在新冠状病毒的影响下,某学校积极响应政府号召,开展了“停课不停学”网上授课工作,为了网上授课工作顺利开展和取得良好成效,该校在授课第一周和授课第二周分别随机抽取部分学生进行“网上授课教学效果反馈”网上调查,并将调查结果绘制成如下两幅不完整的统计图,调查显示:两次调查反馈教学效果为“较差”人数相等,第二周反馈教学效果为“很好”人数比例比第一周多![]() ,请根据调查显示和统计图中的信息解决下列问题:
,请根据调查显示和统计图中的信息解决下列问题:
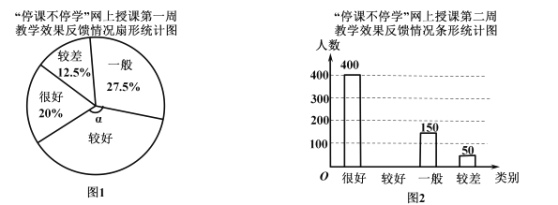
![]() 在图1中,表示“较好”的扇形圆心角
在图1中,表示“较好”的扇形圆心角![]() 的度数为_ 度,并把图2条形统计图补充完整;
的度数为_ 度,并把图2条形统计图补充完整;
![]() 若把调查反馈教学效果“很好”和“较好”作为网上授课成效良好的标准,该校大约有
若把调查反馈教学效果“很好”和“较好”作为网上授课成效良好的标准,该校大约有![]() 名学生,请估计授课第二周学校网上授课成效良好的学生人数;
名学生,请估计授课第二周学校网上授课成效良好的学生人数;
![]() 有一位家长认为,两次调查反馈授课效果为“较差”人数相等,因此学校在一周后调整的措施并没有提高网上授课效果,这位家长分析数据的方法合理吗?请结合统计图,对这位家长分析数据的方法及学校在一周后调整措施对网上授课效果的影响谈谈你的看法.
有一位家长认为,两次调查反馈授课效果为“较差”人数相等,因此学校在一周后调整的措施并没有提高网上授课效果,这位家长分析数据的方法合理吗?请结合统计图,对这位家长分析数据的方法及学校在一周后调整措施对网上授课效果的影响谈谈你的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
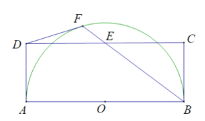
【题目】如图,在矩形ABCD中,边AB是半圆O的直径,点E是CD的中点,BE交半圆O于点F,连接DF.
(1)求证:DF是半圆O的切线;
(2)若AB =8,AD =3,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com