

分析 (1)结论:BF=$\sqrt{2}$CF,如图1中,将△AEC沿AE折叠得到△AEG,连接GF、GE,延长AE、BG交于点H,连接CH,只要证明△BFH是等腰直角三角形即可解决问题.
(2)如图2中,将△AEC沿AE折叠得到△AEG,连接GF、GE,延长AE、BG交于点H,连接CH,只要证明△BFH是等边三角形即可.
(3)首先证明∠FCH=90°,由BF∥CH,得$\frac{CH}{BF}$=$\frac{CE}{BE}$,由FH=2CH,推出BE=2CE,设EC=EG=a,则BC=AC=AG=3a,由△MGE∽△MBE,推出$\frac{EG}{AB}$=$\frac{MG}{MB}$=$\frac{1}{3}$,推出BM=3$\sqrt{7}$,由$\frac{EM}{AM}$=$\frac{MG}{MB}$,推出AM=3ME,列出方程即可求出a,由(2)可知BF=$\frac{2\sqrt{3}}{3}$CF,设CF=x,则BF=$\frac{2\sqrt{3}}{3}$x,在RT△BFC中,根据BF2+CF2=BC2,列出方程即可解决问题.
解答 (1)解:结论:BF=$\sqrt{2}$CF,
理由:如图1中,将△AEC沿AE折叠得到△AEG,连接GF、GE,延长AE、BG交于点H,连接CH.
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵∠ACE=∠AGE=∠ABE,
∴A、B、G、E四点共圆,
∴∠GBE=∠GAE=∠CAE,
∴A、B、H、C四点共圆,
∴∠AHB=∠ACB=45°,
∵∠BFH=∠BAC=90°,
∴∠FBH=∠FHB=45°,
∵∠CFE=∠HFG=45°,
∴∠GFB=∠GFH=45°,
∴FG⊥BH,
在RT△BFG中,∵∠FBG=∠BFG=45°,
∴tan45°=$\frac{FG}{BF}$,
∴BF=$\sqrt{2}$FG,
∵FG=FC
∴BF=$\sqrt{2}$CF.
故答案为BF=$\sqrt{2}$CF.
(2)证明:如图2中,将△AEC沿AE折叠得到△AEG,连接GF、GE,延长AE、BG交于点H,连接CH.
∵AB=AC,∠BAC=60°,
∴∠ABC=∠ACB=60°,
∵∠ACE=∠AGE=∠ABE,
∴A、B、G、E四点共圆,
∴∠GBE=∠GAE=∠CAE,
∴A、B、H、C四点共圆,
∴∠AHB=∠ACB=60°,
∵∠BFH=∠BAC=60°,
∵∠CFE=∠HFG=30°,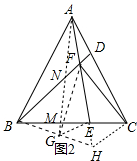
∴∠BFG=∠GFH=30°,
∴FG⊥BH,
在RT△BFG中,∵sin60°=$\frac{FG}{BF}$,
∴BF=$\frac{2\sqrt{3}}{3}$FG,
∵FG=FC,
∴BF=$\frac{2\sqrt{3}}{3}$CF.
(3)如图2中,由(2)可知△BFH是等边三角形,
∵A、B、H、C四点共圆,
∴∠AHC=∠ABC=60°,
∵∠HFC=30°,
∴∠FCH=90°,
∵∠BFC+∠HCF=180°,
∴BF∥CH,
∴$\frac{CH}{BF}$=$\frac{CE}{BE}$,
∵FH=2CH,
∴BE=2CE,设EC=EG=a,则BC=AC=AG=3a,
∵∠ABM=∠MGE,∠BMA=∠GME,
∴△MGE∽△MBE,
∴$\frac{EG}{AB}$=$\frac{MG}{MB}$=$\frac{1}{3}$,
∵GM=$\sqrt{7}$,
∴BM=3$\sqrt{7}$,
∵$\frac{EM}{AM}$=$\frac{MG}{MB}$,
∴AM=3ME,
∴3a-$\sqrt{7}$=3(3a-3$\sqrt{7}$-a),
∴a=$\frac{8}{3}$$\sqrt{7}$,
∴BC=3a=8$\sqrt{7}$,
由(2)可知BF=$\frac{2\sqrt{3}}{3}$CF,设CF=x,则BF=$\frac{2\sqrt{3}}{3}$x,
在RT△BFC中,∵BF2+CF2=BC2,
∴($\frac{2\sqrt{3}}{3}$x)2+x2=(8$\sqrt{7}$)2,
解得x=±8$\sqrt{3}$,
∵x>0,
∴x=8$\sqrt{3}$,
∴CF=8$\sqrt{3}$.
点评 本题考查翻折变换、四点共圆、等边三角形、等腰直角三角形的性质、30度角所对的直角边等于斜边的一半、勾股定理等知识,解题的关键是利用翻折变换添加辅助线,学会利用参数解决问题,学会用方程的思想思考问题,属于中考压轴题.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向上平移2个单位 | B. | 向下平移4个单位 | C. | 向下平移2个单位 | D. | 向上平移4个单位 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
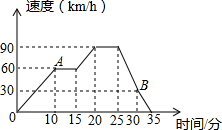 如图是一辆汽车的速度随时间变化而变化的图象,回答下面的问题:
如图是一辆汽车的速度随时间变化而变化的图象,回答下面的问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com