
【题目】如果有一列数,从这列数的第2个数开始,每一个数与它的前一个数的比等于同一个非零的常数,这样的一列数就叫做等比数列(Geometric Sequences).这个常数叫做等比数列的公比,通常用字母q表示(q≠0).
(1)观察一个等比列数1,![]() ,…,它的公比q= ;如果an(n为正整数)表示这个等比数列的第n项,那么a18= ,an= ;
,…,它的公比q= ;如果an(n为正整数)表示这个等比数列的第n项,那么a18= ,an= ;
(2)如果欲求1+2+4+8+16+…+230的值,可以按照如下步骤进行:
令S=1+2+4+8+16+…+230…①
等式两边同时乘以2,得2S=2+4+8+16++32+…+231…②
由② ﹣ ①式,得2S﹣S=231﹣1
即(2﹣1)S=231﹣1
所以 ![]()
请根据以上的解答过程,求3+32+33+…+323的值;
(3)用由特殊到一般的方法探索:若数列a1,a2,a3,…,an,从第二项开始每一项与前一项之比的常数为q,请用含a1,q,n的代数式表示an;如果这个常数q≠1,请用含a1,q,n的代数式表示a1+a2+a3+…+an.
科目:初中数学 来源: 题型:
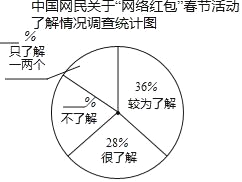
【题目】“网络红包”是互联网运营商、商家通过组织互联网线上活动、派发红包的互联网工具,是朋友间互道祝福的表达形式之一.“网络红包”春节活动已经逐渐深入到大众的生活中,得到了人们较为广泛的关注.根据某咨询公司(2018年中国春节“网络红包”专题调查报告》显示:在接受调查的8万名网民中,对“网络红包”春节话动了解程度的占比方面,“较为了解”和“很了解”的网民共占比64%,分别占比36%和28%.在“不了解”和“只了解一两个“的受访网民中,“不了解”的网民人数比“只了解一两个”的网民人数多25%.如图是该咨询公司绘制的“中国网民关于‘网络红包’春节活动了解情况调查”统计图(不完整).
请根据以上信息解答下列问题:
(1)在受访的网民中,“不了解”和“只了解一两个”的网民人数共有 万人,其中“不了解”的网民人数是 万人;
(2)请将扇形统计图补充完整;
(3)2017除夕晚上小聪和爸爸、妈妈一起玩微信抢红包游戏,他们约定由爸爸在家人微信群中先后发两次“拼手气红包”,每次发放的红包数是3个,每个红包抽到的金额随机(每两个红包的金额都不相等),每次谁抽到红包的金额最大谁就是“手气最佳”者,求两次游戏中小聪都能获得“手气最佳”的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC,BD相交于点O,∠ADB=30°,E为BC边上一点,∠AEB=45°,CF⊥BD于F.下列结论:①BE=CD,②BF=3DF,③AE=![]() AO,④CE=CF.正确的结论有( )
AO,④CE=CF.正确的结论有( )
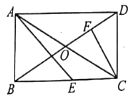
A. ①②B. ②③C. ①②④D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点C是直线AB上一点,AC=6cm,BC=4cm,点M、N分别是AC、BC的中点;
(1)如图,点C在线段AB上,求线段MN的长;
(2)若点C在线段AB的延长线上,其他条件不变,则线段MN的长为_______cm.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的中线BD,CE交于点O,F,G分别是BO,CO的中点.
(1)填空:四边形DEFG是 四边形.
(2)若四边形DEFG是矩形,求证:AB=AC.
(3)若四边形DEFG是边长为2的正方形,试求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,同学们利用如图所示的程序进行计算,计算按箭头指向循环进行.
如,当初始输入5时,即![]() =5,第1次计算结果为16,第2次计算结果为8,第3次计算结果为4,…
=5,第1次计算结果为16,第2次计算结果为8,第3次计算结果为4,…

(1)当初始输入1时,第1次计算结果为 ;
(2)当初始输入4时,第3次计算结果为 ;
(3)当初始输入3时,依次计算得到的所有结果中,有 个不同的值,第20次计算结果为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
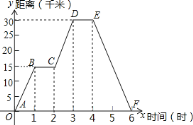
【题目】小明同学骑自行车去滨海港郊游,中途休息了一段时间。如图表示他离家的距离y(千米)与所用的时间s(小时)之间关系的函数图像
(1)根据图像回答:小明家离滨海港 千米,小明到达滨海港时用了 小时;
(2)直线CD的函数解析式为 ;
(3)小明出发几小时,离家12千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com