
【题目】如图,在△ABC中,AB=AC,∠BAC=45°,将△ABC绕点A逆时针方向旋转得△AEF,其中,E,F是点B,C旋转后的对应点,BE,CF相交于点D.若四边形ABDF为菱形,则∠CAE的大小是( )
![]()
A. 45°B. 60°C. 75°D. 90°
科目:初中数学 来源: 题型:
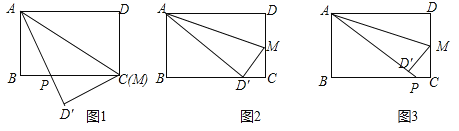
【题目】已知长方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,由
上,由![]() 往
往![]() 运动,速度为
运动,速度为![]() ,运动时间为
,运动时间为![]() 秒,将
秒,将![]() 沿着
沿着![]() 翻折至
翻折至![]() ,点
,点![]() 对应点为
对应点为![]() ,
,![]() 所在直线与边
所在直线与边![]() 交与点
交与点![]() ,
,
(1)如图![]() ,当
,当![]() 时,求证:
时,求证:![]() ;
;
(2)如图![]() ,当
,当![]() 为何值时,点
为何值时,点![]() 恰好落在边
恰好落在边![]() 上;
上;
(3)如图![]() ,当
,当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:
(![]() )如图①,
)如图①,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上任意一点,则
边上任意一点,则![]() 的最小值为__________.
的最小值为__________.
(![]() )如图②,矩形
)如图②,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、点
、点![]() 分别在
分别在![]() 、
、![]() 上,求
上,求![]() 的最小值.
的最小值.
(![]() )如图③,矩形
)如图③,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,且
边上一点,且![]() ,点
,点![]() 是
是![]() 边上的任意一点,把
边上的任意一点,把![]() 沿
沿![]() 翻折,点
翻折,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() 、
、![]() ,四边形
,四边形![]() 的面积是否存在最小值,若存在,求这个最小值及此时
的面积是否存在最小值,若存在,求这个最小值及此时![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点P,Q分别在BC,AC上,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下面结论错误是( )
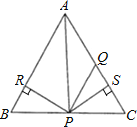
A. △BPR≌△QPSB. AS=ARC. QP∥ABD. ∠BAP=∠CAP
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax+bx+4(a≠0)过点A(1, ﹣1),B(5, ﹣1),与y轴交于点C.
(1)求抛物线表达式;
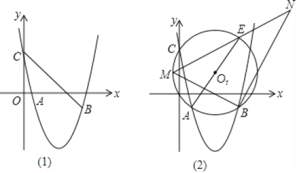
(2)如图1,连接CB,以CB为边作CBPQ,若点P在直线BC下方的抛物线上,Q为坐标平面内的一点,且CBPQ的面积为30,
①求点P坐标;
②过此二点的直线交y轴于F, 此直线上一动点G,当GB+![]() 最小时,求点G坐标.
最小时,求点G坐标.
(3)如图2,⊙O1过点A、B、C三点,AE为直径,点M为 上的一动点(不与点A,E重合),∠MBN为直角,边BN与ME的延长线交于N,求线段BN长度的最大值
查看答案和解析>>
科目:初中数学 来源: 题型:
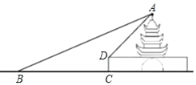
【题目】在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
(1)求城门大楼的高度;
(2)每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出学习了全等三角形的判定方法(“SSS”“SAS”“ASA”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
初步思考:将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠ABC=∠DEF.然后对∠ABC进行分类,可分为“∠ABC是锐角、直角、钝角”三种情况进行探究。
第一种情况:当∠ABC是锐角时,AB=DE不一定成立;
第二种情况:当∠ABC是直角时,根据“HL”,可得△ABC≌ΔDEF,则AB=DE;
第三种情况:当∠ADC是钝角时,则AB=DE.
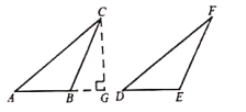
如图,在△ABC和△DEF中,AC=DF,BC=EF,∠ABC=∠DEF,且∠ABC是钝角,求证:AB=DE.
方法归纳化归是一种有效的数学思维方式,一般是将未解决的问题通过交换转化为已解决的问题.观群发现第三种情况可以转化为第二种情况,如图,过点C作CG⊥AB交廷长线于点G.
(1)在ΔDEF中用尺规作出DE边上的高FH,不写作法,保留作图痕迹;
(2)请你完成(1)中作图的基础上,加以证明AB=DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
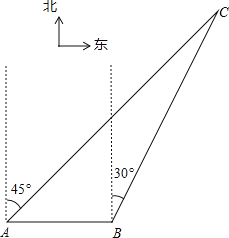
【题目】如图,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场.若渔政310船航向不变,航行半小时后到达B处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数 y kx b k 0的图象与反比例函数 y ![]() m 0的图象交于 A (-1,-1),B (n,2)两点.
m 0的图象交于 A (-1,-1),B (n,2)两点.
(1)求反比例函数和一次函数的表达式;
(2)点 P 在 x 轴上,过点 P 做垂直于 x 轴的直线 l,交直线 AB 于点 C,若AB=2AC,请直接写出点 C 的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com