
分析 (1)先计算△=m2-4(m-2)=m2-4m+8,配方得到△=(m-2)2+4,由于(m-2)2≥0,则(m-2)2+4>0,即△>0,根据△的意义即可得到无论m取何值,该方程总有两个不相等的实数根;
(2)利用根与系数的关系,结合等式x12+x22=-3x1x2即可求解.
解答 (1)证明:∵△=m2-4×1×(m-2)=m2-4m+8=(m-2)2+4>0,
∴不论m取何实数,该方程都有两个不相等的实数根;
(2)解:x1+x2=-m,x1x2=m-2,
∵x12+x22=-3x1x2,
∴${{(x}_{1}{+x}_{2})}^{2}$-2x1 x2=-3x1 x2
∴${{(x}_{1}{+x}_{2})}^{2}$=-x1 x2
∴m2=2-m,
∴m2+m-2=0,
∴(m+2)(m-1)=0,
∴m=-2或1.
点评 本题主要考查一元二次方程根的判别式和根与系数的关系的应用,能够综合运用公式是解答此题的关键.


科目:初中数学 来源: 题型:填空题
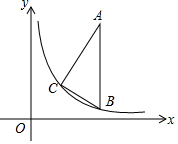 如图,在直角△ABC中,∠C=90°,∠A=30°,AB∥y轴,且AB=6,顶点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,且点B的横坐标为2$\sqrt{3}$,则k=$\sqrt{3}$.
如图,在直角△ABC中,∠C=90°,∠A=30°,AB∥y轴,且AB=6,顶点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,且点B的横坐标为2$\sqrt{3}$,则k=$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
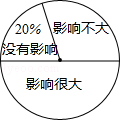 近年来,学校对“在初中数学教学时总使用计算器是否直接影响学生计算能力的发展”这一问题密切关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
近年来,学校对“在初中数学教学时总使用计算器是否直接影响学生计算能力的发展”这一问题密切关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:| 看法 | 没有影响 | 影响不大 | 影响很大 |
| 学生人数(人) | 40 | 60 | m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
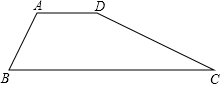 如图,已知四边形ABCD中,AD∥BC,AB=AD.
如图,已知四边形ABCD中,AD∥BC,AB=AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
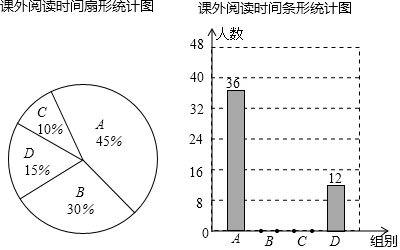
| 组别 | 课外阅读t(单位:时) |
| A | X<2 |
| B | 2≤x<3 |
| C | 3≤x<4 |
| D | x≥4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.
如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com