
 如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,使AE=CF,连接AF,BE相交于点P.
如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,使AE=CF,连接AF,BE相交于点P.分析 (1)依据等边三角形的性质得到AB=AC,∠C=∠CAB,然后依据SAS可证明△ABE≌△CAF,依据全等三角形的性质可得到∠ABE=∠CAF,最后,再依据三角形的外角的性质求解即可;
(2)先证明△APE∽△ACF,依据相似三角形的性质得到$\frac{AP}{AC}$=$\frac{AE}{AF}$,从而可得到问题的答案.
解答 解:(1)∵△ABC为等边三角形,
∴AB=AC,∠C=∠CAB=60°,
在△ABE和△CAF中,$\left\{\begin{array}{l}{AB=AC}\\{∠C=∠CAB}\\{AE=CF}\end{array}\right.$,
∴△ABE≌△CAF,
∴AF=BE,∠ABE=∠CAF.
又∵∠APE=∠BPF=∠ABP+∠BAP,
∴∠APE=∠BAP+∠CAF=60°,
∴∠APB=180°-∠APE=120°
(2)∵∠C=∠APE=60°,∠PAE=∠CAF,
∴△APE∽△ACF,
∴$\frac{AP}{AC}$=$\frac{AE}{AF}$,即$\frac{AP}{6}$=$\frac{2}{AF}$,
∴AP•AF=12.
点评 本题主要考查的是全等三角形的性质和判定、相似三角形的性质和判定,熟练掌握相关知识是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当3CQ=CE时,EP+BP=8.
如图,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当3CQ=CE时,EP+BP=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
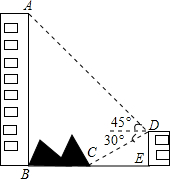 如图,大楼沿右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同-水平直线上.己知AB=80m,DE=10m,求障碍物B、C两点间的距离(结果精确到0.1m)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,大楼沿右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同-水平直线上.己知AB=80m,DE=10m,求障碍物B、C两点间的距离(结果精确到0.1m)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com