
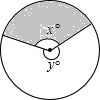
 如图,扇子的圆心角为x°,余下的圆心角为y°,x与y的比通常用黄金比来设计,这样的扇子造型美观,则x的值为多少?(精确到0.1)
如图,扇子的圆心角为x°,余下的圆心角为y°,x与y的比通常用黄金比来设计,这样的扇子造型美观,则x的值为多少?(精确到0.1)  教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若|a|=|b|,则a=b | B. | 若a<b,则|a|<|b| | ||
| C. | 若a、b互为相反数,则$\frac{a}{b}$=-1 | D. | 若a>|b|,则a>b |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
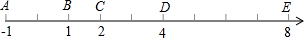 如图,在一条数轴上有依次排列的5台机床A、B、C、D、E在工作,现要设置一个零件供应站P,使这5台机床到供应站P的距离总和最小,供应站P建在哪?最小值为多少?
如图,在一条数轴上有依次排列的5台机床A、B、C、D、E在工作,现要设置一个零件供应站P,使这5台机床到供应站P的距离总和最小,供应站P建在哪?最小值为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com