
����Ŀ����ֱ֪��l��y=kx��������C��y=ax2+bx+1��
��1����k=1��b=1ʱ��������C��y=ax2+bx+1�Ķ�����ֱ��l��y=kx�ϣ���a��ֵ��
��2������ֱ��l����ƽ��k2+1����λ���ȵõ�ֱ��r�������۷���ʵ��kȡ��ֵ��ֱ��r��������C��ֻ��һ�����㣻
��i����������ߵĽ���ʽ��
��ii����P�Ǵ�����������һ�㣬����P��PQ��y������ֱ��y=2���ڵ�Q��OΪԭ�㣬
��֤��OP=PQ��
���𰸡�������a=��![]() ����������i��y=��
����������i��y=��![]() x2+1����ii��֤��������.
x2+1����ii��֤��������.
��������
��1������a��ʾ�������ߵĶ�������,�ٴ���ֱ�߷��̿����a��ֵ,
��2����i������kΪ�������ʵ��,��ȡk=1��k=2,������������ʽ��ȥy,�õ���һԪ���η�����������ȵ�ʵ�����ɵõ���������a��b�ķ���,�����a��b��ֵ,������Ò����߽���ʽ; ��ii�����P������,����OP,��P��PQ��ֱ��y=2,��PD��x���ڵ�D,�ɷֱ��ʾ��OP��PQ,��֤�������
�⣺��1����k=1��b=1����ã������ߵĽ���ʽΪy=ax2+x+1��ֱ�ߵĽ���ʽΪy=x��
��y=ax2+x+1=a��x+ ![]() ��2+1��
��2+1�� ![]() ��
��
�������ߵĶ���Ϊ���� ![]() ��1��
��1�� ![]() ����
����
�������ߵĶ�����ֱ��y=x�ϣ�
�ੁ ![]() =1��
=1�� ![]() ��
��
��ã�a=��![]() ��
��
��2����i����ֱ��y=kx����ƽ��k2+1����λ������ֱ�ߵĽ���ʽΪy=kx+k2+1��
�����۷���ʵ��kȡ��ֵ��ֱ���������߶�ֻ��һ�����㣬
������kx+k2+1=ax2+bx+1��������ȵ�ʵ��������ax2+��b��k��x��k2=0��������ȵ�ʵ������
���=��b��k��2+4ak2=��4a+1��k2��2bk+b2=0��
�����۷���ʵ��kȡ��ֵʱ����4a+1��k2��2bk+b2=0�������
��4a+1=0��b=0��
��a=�� ![]() ��b=0��
��b=0��
�������ߵĽ���ʽΪy=��![]() x2+1��
x2+1��
��ii��֤�����������⣬����ͼ����ͼ��ʾ��
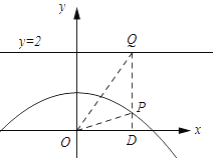
���P��������x���� ![]() x2+1�����Q��������x��2����D��x��0����
x2+1�����Q��������x��2����D��x��0����
��PD=|�� ![]() x2+1|��OD=|x|��QP=2������
x2+1|��OD=|x|��QP=2������ ![]() x2+1��=
x2+1��= ![]() x2+1��
x2+1��
��Rt��OPD�У����ݹ��ɶ����ã�OP= ![]() =
= ![]() =
= ![]() x2+1��
x2+1��
��OP=PQ



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD�ֱ����ԲOO���ڵ�A��D��BC����O�ڵ�E����AB=4��CD=9������O�İ뾶Ϊ��������
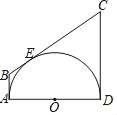
A. 12 B. ![]()
![]() C. 6 D. 5
C. 6 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ÿ�궼������ϣ��������������ȥ������Σ���15֧���������ÿ����֮�䶼����һ�����±���ȥ��������ֶ���Ļ��ְ�
���� | �������� | ʤ�� | ���� | ���� |
A | 14 | 10 | 4 | 24 |
B | 14 | 9 | 5 | 23 |
C | 14 | 4 | 10 | 18 |
D | 14 | 0 | 14 | 14 |
��1��ȥ��ij�ӵ��ܻ���Ϊ20�֣���ö��ڱ�����ʤ�˶��ٳ���
��2�����꣬�����Ķ����ȥ���������ӣ��������ޣ���ί����������ι�����40��������������������ƽ���ֳ�4��С�飬��С��ÿ����֮�䶼����һ����������ȥ�������˶���֧���飿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��, ��֪��ABC��, ��BAC=90��, AB=AC, AE�ǹ�A��һ��ֱ��, ��B��C��AE�����, BD��AE��D, CE��AE��E.

(1)��֤: BD=DE+CE.
(2)��ֱ��AE��A����ת��ͼ��λ��ʱ(BD<CE), ������������, ��BD��DE��CE��������ϵ���? �����֤����
(3)��ֱ��AE��A����ת��ͼ��λ��ʱ(BD>CE), ������������, ��BD��DE��CE��������ϵ���? ��ֱ��д�����, ����֤��.
(4)�������ϵ����ۣ����ü������Ա���BD��DE,CE��������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
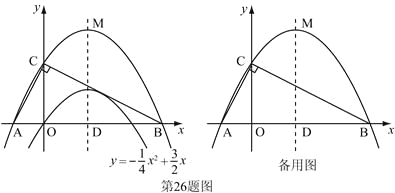
����Ŀ������������12�֣���֪���κ���![]() ��ͼ����ͼ.
��ͼ����ͼ.
��1�������ĶԳ�����![]() �ύ��D�����ꣻ
�ύ��D�����ꣻ
��2�����������������ĶԳ�������ƽ�ƣ���ƽ�ƺ����������![]() �ᣬ
�ᣬ![]() ��Ľ���ֱ�ΪA��B��C���㣬����ACB=90�������ʱ�����ߵĽ���ʽ��
��Ľ���ֱ�ΪA��B��C���㣬����ACB=90�������ʱ�����ߵĽ���ʽ��
��3���裨2����ƽ�ƺ�������ߵĶ���ΪM����ABΪֱ����DΪԲ������D�����ж�ֱ��CM����D��λ�ù�ϵ����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
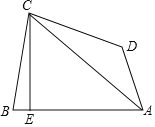
����Ŀ����ͼ�����ı���ABCD�У�AC���ı��εĶԽ��ߣ���CAD=30�㣬����C��CE��AB�ڵ�E����B=2��BAC����ADC����BAC=90�㣬��AB=20��CD=16����BE�ij�Ϊ____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
(1)(2x2y)3(3x2y)
(2)(36x3-24x2+2x)��4x
(3)(2x+y+1)(2x-y-1)
(4)(-3ax)2(5a2-3ax3)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ߵ�����Ů��������е�һ��������Ŀ������������ɸߡ�������ƽ�иܼ�����֧����ɣ��˶�Ա�ɸ����Լ������ߺ�ϰ���ڹ涨��Χ�ڵ��ڸߡ������ܼ�ľ��룮ij��ȤС����ݸߵ����ĵ�һ�ֽ���ͼ������������ѧ���⣬������
��ͼ��ʾ��������A��B�����ľ���Ϊ90cm�����ϵ�C��ֱ��AB�ľ���CE�ij�Ϊ155cm���߸��ϵ�D��ֱ��AB�ľ���DF�ij�Ϊ234cm����֪�ܵ�֧��AC��ֱ��AB�ļнǡ�CAEΪ82.4�����߸ܵ�֧��BD��ֱ��AB�ļнǡ�DBFΪ80.3������ߡ��ܼ��ˮƽ����CH�ij����������ȷ��1cm���ο�����sin82.4���0.991��cos82.4���0.132��tan82.4���7.500��sin80.3���0.983��cos80.3���0.168��tan80.3���5.850��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����÷��ѧΪ�˷ḻѧ���Ŀ�������ƻ�����Χ����й����幩������ȤС��ʹ�ã�������3��Χ���5���й���������98Ԫ��������8��Χ���3���й���������158Ԫ����1����ÿ��Χ���ÿ���й����������Ԫ����2����÷��ѧ��������Χ����й����干40�����ܷ��ò�����550Ԫ����ô��÷��ѧ�����Թ�����ٸ�Χ��?
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com