
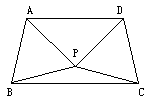
如图,△PAB与△PDC是两个全等的等边三角形,且PA⊥PD,有下列四个结论:
①∠PBC=![]() ;
;
②AD∥BC;
③直线PC与AB垂直;
④四边形ABCD是轴对称图形.
其中正确结论的个数是
[ ]
|
选D,4个结论都正确. △PAB与△PDC是两个全等的等边三角形,则AB=BP=AP=CP=DP=CD. ∠BPC=360°-∠APB-∠CPD-∠APD=150°,∵PB=PC,∴∠PBC=∠PCB= △APD是等腰直角三角形,∴∠PAD=45°,∴∠DAB=∠PAD+∠BAP=45°+60°=105°,∠ABC=∠ABP+∠PBC=60°+15°=75°,∴∠DAB+∠ABC=105°+75°=180°,∴AD∥BC,②正确; ∠ABC=75°,∠PCB=∠PBC=15°,∴∠ABC与∠PCB互余,则∠ABC与∠PCB构成的三角形是直角三角形,③正确; 由AD∥BC知四边形ABCD是梯形,可以计算出∠ABC=∠DCB=75°,∴四边形ABCD是等腰梯形,等腰梯形是轴对称图形,④正确.
|


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
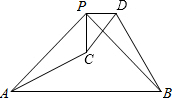 (2012•新化县二模)如图,△PAB与△PCD都是等腰直角三角形,∠APB=∠CPD=90°,连接AC、BD,试猜想线段AC和BD的数量关系,并证明你的猜想.
(2012•新化县二模)如图,△PAB与△PCD都是等腰直角三角形,∠APB=∠CPD=90°,连接AC、BD,试猜想线段AC和BD的数量关系,并证明你的猜想.查看答案和解析>>
科目:初中数学 来源:2012年湖南省娄底市新化县中考数学二模试卷(解析版) 题型:解答题
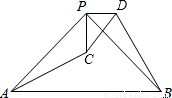
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com