
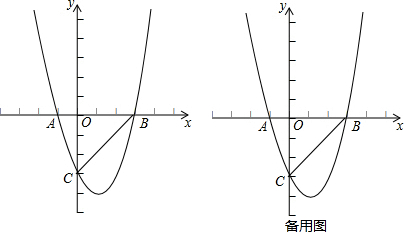
分析 (1)先表示出C点坐标(0,-3m),再证明△OBC为等腰直角三角形得到OB=OC=3m,则B(3m,0),然后把B(3m,0)代入y=x2+(m-3)x-3m得关于m的方程,解方程求出m,从而得到B点坐标;
(2)抛物线的解析式为y=x2-2x-3,分别计算x=-2和x=2时的函数值,利用函数图象,由于当-2<x<2时,x2+(m-3)x-3m<kx+b,所以直线y=kx+b经过点(-2,5),(2,-3),然后利用待定系数法确定一次函数解析式;
(3)讨论:当BC为对角线时,如图1,设P(t,-2t+1),利用平行四边形的性质,通过点C平移到点P的坐标变化情况得到点B平移到点Q的坐标变换规律,从而得到点Q(3-t,2t-4),然后把Q(3-t,2t-4)代入y=x2-2x-3得(3-t)2-2(3-t)-3=2t-4;当BC边时,如图2,设P(t,-2t+1),利用同样的方法得到点Q(3+t,-2t+4),然后把Q(3+t,-2t+4)代入y=x2-2x-3得(3+t)2-2(3+t)-3=-2t+4,最后分别解关于t的方程,从而得到P点坐标.
解答 解:*(1)当x=0时,y=x2+(m-3)x-3m=-3m,则C(0,-3m),
∵∠ABC=45°,
∴△OBC为等腰直角三角形,
∴OB=OC=3m,则B(3m,0),
把B(3m,0)代入y=x2+(m-3)x-3m得9m2+3m(m-3)-3m=0,
整理得m2-m=0,解得m1=0(舍去),m2=1,
∴m的值为1,B(3,0);
(2)抛物线的解析式为y=x2-2x-3,
当x=-2时,y=x2-2x-3=5;当x=2时,y=x2-2x-3=-3,
∵只有当-2<x<2时,x2+(m-3)x-3m<kx+b,
∴直线y=kx+b经过点(-2,5),(2,-3),
∴$\left\{\begin{array}{l}{-2k+b=5}\\{2k+b=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-2}\\{b=1}\end{array}\right.$,
∴一次函数解析式为y=-2x+1;
(3)存在.
当BC为对角线时,如图1,
设P(t,-2t+1),
∵点C(0,-3)向右平移t个单位,向上平移(-2t+4)个单位得到点P(t,-2t+1),则点B(3,0)向左平移t个单位,向下平移(-2t+4)个单位得到点Q(3-t,2t-4),
把Q(3-t,2t-4)代入y=x2-2x-3得(3-t)2-2(3-t)-3=2t-4,
整理得t2-6t+4=0,解得t1=3-$\sqrt{5}$,m2=3+$\sqrt{5}$,此时P点坐标为(3-$\sqrt{5}$,-5+2$\sqrt{5}$)或(3+$\sqrt{5}$,-5-2$\sqrt{5}$);
当BC边时,如图2,
设P(t,-2t+1),
∵点C(0,-3)向右平移t个单位,向上平移(-2t+4)个单位得到点P(t,-2t+1),则点B(3,0)向右平移t个单位,向上平移(-2t+4)个单位得到点Q(3+t,-2t+4),
把Q(3+t,-2t+4)代入y=x2-2x-3得(3+t)2-2(3+t)-3=-2t+4,
整理得t2+6t-4=0,解得t1=-3-$\sqrt{13}$,m2=-3+$\sqrt{13}$,此时P点坐标为(-3-$\sqrt{13}$,-5+2$\sqrt{13}$)或(-3-$\sqrt{13}$,-5-2$\sqrt{13}$),
综上所述,满足条件的P点坐标为(3-$\sqrt{5}$,-5+2$\sqrt{5}$)或(3+$\sqrt{5}$,-5-2$\sqrt{5}$)或(-3-$\sqrt{13}$,-5+2$\sqrt{13}$)或(-3-$\sqrt{13}$,-5-2$\sqrt{13}$).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和平行四边形的性质;会利用待定系数法求函数解析式;理解点平移的坐标规律和坐标与图形性质;会运用分类讨论的思想解决数学问题.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:解答题
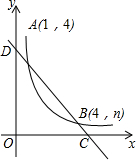 如图,直线y1=ax+b与反比例函数y2=$\frac{m}{x}$(x>0)的图象交于A(1,4)、B(4,n)两点,与x轴、y轴交于C、D两点.
如图,直线y1=ax+b与反比例函数y2=$\frac{m}{x}$(x>0)的图象交于A(1,4)、B(4,n)两点,与x轴、y轴交于C、D两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
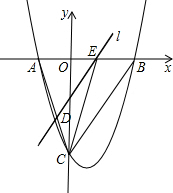 如图,抛物线y=$\frac{4}{3}$x2-$\frac{8}{3}$x-4与x轴交于A,B两点,与y轴交于点C,连接BC,AC.
如图,抛物线y=$\frac{4}{3}$x2-$\frac{8}{3}$x-4与x轴交于A,B两点,与y轴交于点C,连接BC,AC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 城市 | 北京 | 成都 | 深圳 | 长沙 | 上海 | 武汉 | 广州 |
| AQI指数 | 25 | 72 | 49 | 241 | 62 | 185 | 49 |
| A. | 49 | B. | 62 | C. | 241 | D. | 97 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
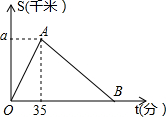 某运动员从起点东胜一中出发,到植物园后,沿比赛路践跑回东胜一中,设该运动员离开起点的路程S(平米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到植物园的平均速度是0.4千米/分,用时35分钟,根据图象提供的信息,解答下列问题:
某运动员从起点东胜一中出发,到植物园后,沿比赛路践跑回东胜一中,设该运动员离开起点的路程S(平米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到植物园的平均速度是0.4千米/分,用时35分钟,根据图象提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
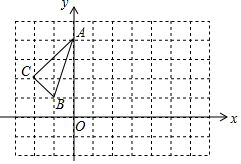 如图,已知△ABC三个顶点的坐标分别为A(0,4),B(-1,1),C(-2,2),将△ABC向右平移4个单位,得到△A′B′C′,点A,B,C的对应点分别为A′、B′、C′,再将△A′B′C′绕点B′顺时针旋转90°,得到△A″B″C″,点A′、B′、C′的对应点分别为A″、B″、C″,则点A″的坐标为(6,0).
如图,已知△ABC三个顶点的坐标分别为A(0,4),B(-1,1),C(-2,2),将△ABC向右平移4个单位,得到△A′B′C′,点A,B,C的对应点分别为A′、B′、C′,再将△A′B′C′绕点B′顺时针旋转90°,得到△A″B″C″,点A′、B′、C′的对应点分别为A″、B″、C″,则点A″的坐标为(6,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
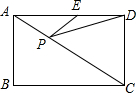 如图,在矩形ABCD中,AD=4,∠DAC=30°,点P、E分别在AC、AD上,则PE+PD的最小值是( )
如图,在矩形ABCD中,AD=4,∠DAC=30°,点P、E分别在AC、AD上,则PE+PD的最小值是( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | $\frac{8\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com