
����Ŀ����ͼ����ˮƽ�����A����һ������������з��������������·����һ�������ߣ��ڵ��������ΪB��������ֱ��AB�ϵ�C������Bһ�ࣩ��ֱ���ϰڷ����ɸ��ǵ�Բ����Ͱ����ͼ����������Ͱ�ڣ���֪AB=4�ף�AC=3�ף�����������߶�OM=5�ף�Բ����Ͱ��ֱ��Ϊ0.5�ף���Ϊ0.3�ף�����������Բ����Ͱ�ĺ�Ⱥ��Բ��ƣ�������ֱ�ڷ�Բ����Ͱ���٣� ����ʱ�������������Ͱ��.
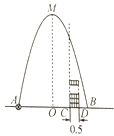
A.7B.8C.9D.10
���𰸡�B
��������
�������ߵĶԳ���Ϊy�ᣬˮƽ����Ϊx�ᣬ����ƽ��ֱ������ϵ�������ʽ�������֪ȷ���������ϵ�����꣬�������ʽȷ�������ߵĽ���ʽ����ԲͰ��ֱ�������ԲͰ����Ե�������ֵ��ȷ��m�ķ�Χ������mΪ���������ó�m��ֵ�����ɵõ��������������Ͱ��ʱ����ֱ�ڷ�Բ����Ͱ������
�Ե�OΪԭ��,AB����ֱ��Ϊx�Ὠ��ֱ������ϵ��
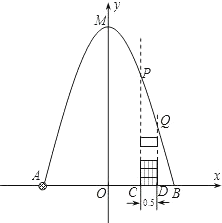
M(0,5),B(2,0),C(1,0),D(![]() ,0)
,0)
�������ߵĽ���ʽΪ![]() ��
��
�����߹���M�͵�B��
��k=5,a=![]()
�������߽���ʽΪ��![]() ��
��
��x=1ʱ��y=![]() ��P��1��
��P��1��![]() ��
��
��x=![]() ʱ��y=
ʱ��y=![]() ��Q(
��Q(![]() ,
,![]() )
)
����ֱ�ڷ�Բ����Ͱm��ʱ�����������Ͱ�ڣ�
������,��, ![]()
![]() m
m![]() ��
��
��ã�![]() m
m![]() ��
��
��m������
��m��ֵΪ8��9��10��11��12.
��m�ĵ���ֱ�ڷ�Բ����Ͱ����8��ʱ�������������Ͱ��.
��ѡB.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��AOB�У���AOB=90�㣬OA=2��OB=1����Rt��AOB�Ƶ�O˳ʱ����ת90����õ�Rt��FOE�����߶�EF�Ƶ�E��ʱ����ת90����õ��߶�ED���քe��O��EΪԲ�ģ�OA��ED��Ϊ�뾶����AF�ͻ�DF������AD����ͼ����Ӱ���ֵ������__��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η��̣�m��1��x2+��m��2��x��1��0��mΪʵ������
��1������������������ȵ�ʵ��������m��ȡֵ��Χ��
��2����m���������ҷ�������������ȵ�����������m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦΪ���˽�ѧ������ѧϰ�����������ľ���������Ա��ಿ��ѧ��������Ϊ�ڰ���ĸ��ٵ��飬�����������ֳ�����A���ţ�B������C���У�D������ݵ��������Ƴ�����������������ͳ��ͼ���������ͳ��ͼ����������⣺
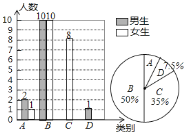
��1�����ε����У�����ʦһ��������______��ѧ����
��2����ͳ��ͼ����������
��3��Ϊ�˹�ͬ����������ʦ��ӱ������A���D��ѧ���зֱ�ѡȡһλͬѧ������һ��һ������������б���������ͼ�ķ�������ѡ����λͬѧǡ������λŮͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
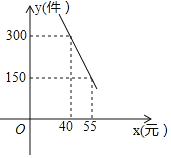
����Ŀ��ij��������һ���ľߴ����ɱ�Ϊ30Ԫ/����ÿ���������![]() �����������۵���
�����������۵���![]() ��Ԫ��֮������һ�κ�����ϵ����ͼ����ͼ��ʾ��
��Ԫ��֮������һ�κ�����ϵ����ͼ����ͼ��ʾ��
��1����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2������涨ÿ�������������240������ô�����۵���Ϊ����Ԫʱ��ÿ���ȡ�����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
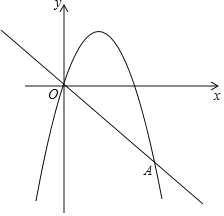
����Ŀ����ͼ����֪һ�κ���y����x����κ���y����x2+bx+c��ͼ���ཻ��ԭ��O����һ��A��4����4����
��1������κ�������ʽ��
��2��ֱ��x��m��x��m+2�ֱ��߶�AO��C��D�������κ���y����x2+bx+c��ͼ���ڵ�E��F����mΪ��ֵʱ���ı���CEFD��ƽ���ı��Σ�
��3���ڵڣ�2����������£���CE��x��Ľ���ΪM������COM�Ƶ�O��ʱ����ת�õ���C��OM�䣬��C�䡢M�䡢F�����һ�ι���ʱ���뻭��ͼ�β�ֱ��д����C��������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����ABCD�У�AB=3��BC=4��ACΪ�Խ��ߣ���DAC�Ľ�ƽ����AE��DC�ڵ�E����CE�ij�Ϊ______��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com