
【题目】(10分)把两个直角边长均为6的等腰直角三角板ABC和EFG叠放在一起(如图①),使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点顺时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).

(1)探究:在上述旋转过程中,BH与CK的数量关系以及四边形CHGK的面积的变化情况(直接写出探究的结果,不必写探究及推理过程);
(2)利用(1)中你得到的结论,解决下面问题:连接HK,在上述旋转过程中,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的![]() ?若存在,求出此时BH的长度;若不存在,说明理由.
?若存在,求出此时BH的长度;若不存在,说明理由.
【答案】(1) BH=CK;(2) 存在,使△GKH的面积恰好等于△ABC面积的![]() 的位置,此时BH的长度为
的位置,此时BH的长度为![]() .
.
【解析】(1)先由ASA证出△CGK≌△BGH,再根据全等三角形的性质得出BH=CK,根据全等得出四边形CKGH的面积等于三角形ACB面积一半;
(2)根据面积公式得出S△GHK=S四边形CKGH-S△CKH=![]() x2-3x+9,根据△GKH的面积恰好等于△ABC面积的
x2-3x+9,根据△GKH的面积恰好等于△ABC面积的![]() ,代入得出方程
,代入得出方程![]() x2-3x+9=
x2-3x+9=![]() ×
×![]() ×6×6,求出即可.
×6×6,求出即可.
解:(1)BH与CK的数量关系:BH=CK,理由是:
连接OC,

由直角三角形斜边上中线性质得出OC=BG,
∵AC=BC,O为AB中点,∠ACB=90°,
∴∠B=∠ACG=45°,CO⊥AB,
∴∠CGB=90°=∠KGH,
∴都减去∠CGH得:∠BGH=∠CGK,
在△CGK和△BGH中
∵ ,
,
∴△CGK≌△BGH(ASA),
∴CK=BH,即BH=CK;
四边形CHGK的面积的变化情况:四边形CHGK的面积不变,始终等于四边形CQGZ的面积,即等于△ACB面积的一半,等于9;
(2)假设存在使△GKH的面积恰好等于△ABC面积的![]() 的位置.
的位置.
设BH=x,由题意及(1)中结论可得,CK=BH=x,CH=CB﹣BH=6﹣x,
∴S△CHK=![]() CH×CK=3x﹣
CH×CK=3x﹣![]() x2,
x2,
∴S△GHK=S四边形CKGH﹣S△CKH=9﹣(3x﹣![]() x2)=
x2)=![]() x2﹣3x+9,
x2﹣3x+9,
∵△GKH的面积恰好等于△ABC面积的![]() ,
,
∴![]() x2﹣3x+9=
x2﹣3x+9=![]() ×
×![]() ×6×6,
×6×6,
解得![]() ,
, ![]() (经检验,均符合题意).
(经检验,均符合题意).
∴存在使△GKH的面积恰好等于△ABC面积的![]() 的位置,此时x的值为
的位置,此时x的值为![]() .
.
“点睛”本题考查了旋转的性质,三角形的面积,全等三角形的性质和判定等知识点,此题有一定的难度,但是一道比较好的题目.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为2的等边△ABC中,AD⊥BC,点P为边AB 上一个动点,过点P作PF∥AC交线段BD于点F,作PG⊥AB交AD于点E,交线段CD于点G,设![]() ,
, ![]() .
.
(1)求证: ![]() ;
;
(2)求y关于x的函数解析式,并写出x的取值范围;
(3)以P、E、F为顶点的三角形与△EDG能否相似?如果能相似,请求出.BP的长,如果不能,请说明理由.

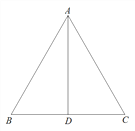
(备用图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数的图象经过A(4,0),B(0,﹣4),C(2,﹣4)三点.
(1)求这个函数的解析式;
(2)求函数图顶点的坐标;
(3)求抛物线与坐标轴的交点围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,属于必然事件的是( )
A. 随时打开电视机,正在播天气预报
B. 抛掷一枚质地均匀的骰子,出现4点朝上
C. 从分别写有3,6两个数字的两张卡片中随机抽出一张,卡片上的数字能被3整除
D. 长度分别是3cm,3cm,6cm的三根木条首尾相接,组成一个三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】扬州市为打造“绿色城市”降低空气中pm2.5的浓度,积极投入资金进行园林绿化工程,已知2014年投资1000万元,预计2016年投资1210万元.若这两年内平均每年投资增长的百分率相同.
(1)求平均每年投资增长的百分率;
(2)经过评估,空气中pm2.5的浓度连续两年较上年下降10%,则两年后pm2.5的浓度比最初下降了百分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 图象的一部分,图象过点A(-3,0),对称轴为直线x=﹣1,给出四个结论:①c>0;②若点B(-1.5,y1)、C(-2.5,y2)为函数图象上的两点,则y1<y2;③2a﹣b=0;④
图象的一部分,图象过点A(-3,0),对称轴为直线x=﹣1,给出四个结论:①c>0;②若点B(-1.5,y1)、C(-2.5,y2)为函数图象上的两点,则y1<y2;③2a﹣b=0;④ ![]() <0.其中正确结论的个数是( )
<0.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com