练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．解下列方程
    （1）x2-3x=1
    （2）3x（x-2）=2（x-2）

    分析 （1）方程整理后，利用公式法求出解即可；
    （2）方程移项后，利用因式分解法求出解即可．

    解答 解：（1）方程整理得：x2-3x-1=0，
    这里a=1，b=-3，c=-1，
    ∵△=9+4=13，
    ∴x=$\frac{3±\sqrt{13}}{2}$，
    解得：x1=$\frac{3+\sqrt{13}}{2}$，x2=$\frac{3-\sqrt{13}}{2}$；
    （2）方程移项得：3x（x-2）-2（x-2）=0，
    分解因式得：（x-2）（3x-2）=0，
    解得：x1=2，x2=$\frac{2}{3}$．

    点评 此题考查了解一元二次方程-因式分解法，熟练掌握因式分解的方法是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．列方程解应用题
    （1）商店对某种商品作调价，按原价的8折出售，此时商品的利润率是10%，此商品的进价为160元．问商品的原价是多少？
    （2）小王、叔叔在400米长的环形跑道上练习跑步，小王每秒跑3米，叔叔每秒跑5米．若两人同时同地同向出发，多长时间两人首次相遇？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．将长方形ABCD沿AE折叠，得到如图所示的图形，若∠CED′=56°，则∠D′AB的大小是（　　）
    A．62°B．28°C．34°D．56°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

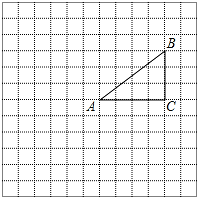    17．正方形网格中的每个小正方形的边长都是1，顶点叫做格点．△ABC的三个顶点A、B、C都在格点上，将△ABC绕点A按顺时针方向旋转90°得到△A′B′C′．
    （1）在正方形网格中，画出△AB′C′．
    （2）求出点B运动到点B′所经过的路径长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．某校的食堂一月份的营业额为2000元，三月份的营业额为2880元，已知平均每个月的增长率相同，请求出平均每个月的增长率为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

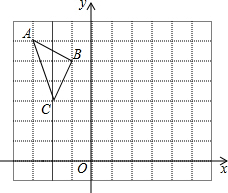    14．如图，已知△ABC请画出△ABC关于y轴对称的图形△A′B′C′并按要求填空．（方格的边长为1）
    A（-3，6），A′（3，6）；
    B（-1，5），B′（1，5）；
    C（-2，3），C′（2，3）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，已知直线AB∥DE，∠ABC=80°，∠CDE=140°，求∠BCD的度数．
    解：过点C作FG∥AB
    因为FG∥AB，AB∥DE（已知）
    所以FG∥DE（平行线的传递性）
    所以∠B=∠BCF（两直线平行，内错角相等）
    ∠CDE+∠DCF=180°（两直线平行，同旁内角互补）
    又因为∠B=80°，∠CDE=140°（已知）
    所以∠BCF=80°（等量代换）
    ∠DCF=40°（等式性质）                  
    所以∠BCD=40°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．如图，在△ABC中，∠B=45°，∠BAC=30°，AB=6+2$\sqrt{3}$，AD是∠BAC的平分线，若P、Q分别是AD和AC的动点，则PC+PQ的最小值是2$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．二次函数y=ax2+bx+c的图象与抛物线y=-x2的形状相同，当顶点坐标为（-1，3）时，相应的二次函数解析式为y=-（x+1）2+3或y=（x+1）2+3．

    查看答案和解析>>

    同步练习册答案