
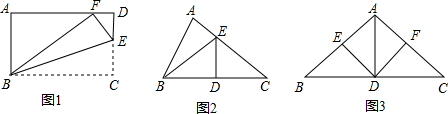
(1)(3分)如图①,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D.
求证:AB2=AD·AC;
(2)(4分)如图②,在Rt△ABC中,∠ABC=90°,点D为BC边上的点,BE⊥AD于点E,延长BE交AC
于点F. ,求
,求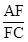 的值;
的值;
(3)(5分) 在Rt△ABC中,∠ABC=90°,点D为直线BC上的动点(点D不与B、C重合),直线BE⊥AD
于点E,交直线AC于点F。若 ,请探究并直接写出
,请探究并直接写出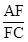 的所有可能的值(用含n的式子表
的所有可能的值(用含n的式子表
示),不必证明.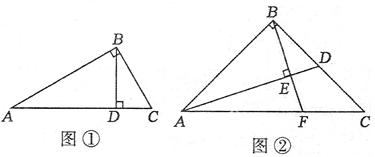
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
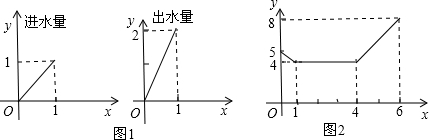
 某中学开展“五比五创”演讲比赛活动,九(1)班准备根据根据平时练习成绩准备从张华、李明2名选手选出一名参加比赛,他们两人的五次平时成绩(满分20分)如图所示.
某中学开展“五比五创”演讲比赛活动,九(1)班准备根据根据平时练习成绩准备从张华、李明2名选手选出一名参加比赛,他们两人的五次平时成绩(满分20分)如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
 线段CA上由点C向点A运动.
线段CA上由点C向点A运动.查看答案和解析>>
科目:初中数学 来源: 题型:
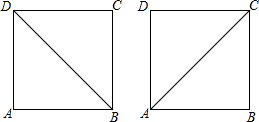 用对角线把多边形分成几个三角形,叫做“多边形的三角剖分”.如图,凸四边形ABCD,有两种剖分方法:(如图示)20世纪,数学家乌尔班发现并证明了下面的公式:
用对角线把多边形分成几个三角形,叫做“多边形的三角剖分”.如图,凸四边形ABCD,有两种剖分方法:(如图示)20世纪,数学家乌尔班发现并证明了下面的公式:| Dn+1 |
| Dn |
| 4n-6 |
| n |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com