练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．先化简，再求值：$\frac{x+1}{1-x}$-$\frac{x+1}{{x}^{2}-1}$，其中x=2．

    分析 先根据分式混合运算的法则把原式进行化简，再把x=2代入进行计算即可．

    解答 解：原式=$\frac{x+1}{1-x}$-$\frac{1}{x-1}$
    =$\frac{x+1}{1-x}$+$\frac{1}{1-x}$
    =$\frac{x+2}{1-x}$，
    当x=2时，原式=$\frac{2+2}{1-2}$=-4．

    点评 本题考查的是分式的化简求值熟知分式混合运算的法则是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    20．下列方程中，不是二元一次方程组的是（　　）
    A．$\left\{\begin{array}{l}x+2y=0\\ 2x+y=1\end{array}\right.$B．$\left\{\begin{array}{l}{x=0}\\{y-x+5=0}\end{array}\right.$C．$\left\{\begin{array}{l}x-2y-1=0\\-x=y+2\end{array}\right.$D．$\left\{\begin{array}{l}x+y=4\\ 2x=z-2y\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列计算，正确的是（　　）
    A．（-$\sqrt{3}$）2=-3B．$\sqrt{（-3）^{2}}$=-3C．（2$\sqrt{6}$）2=24D．$\sqrt{（π-3.2）^{2}}$=π-3.2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．已知二次函数y=（x-1）（x-a-1）（a为常数，且a＞0）．
    （1）求证：不论a为何值，该二次函数的图象总经过x轴上一定点；
    （2）设该函数图象与x轴的交点为A、B（点A在点B的左侧），与y轴的交点为C，△ABC的面积为1．
    ①求a的值；
    ②D是该函数图象上一点，且点D的横坐标是m，若S△ABD=$\frac{1}{8}$S△ABC，直接写出m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

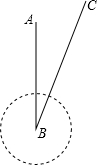    17．台风是一种自然灾害，它以台风中心为圆心在数十千米范围内形成气旋风暴，有极强的破坏力，据气象观察，距沿海某城市A正南256千米的B处有一台风中心，其中心最大风力为12级，每远离台风中心20千米，风力就会减弱一级，该台风中心正以15千米/时的速度沿北偏东30°方向向C移动，且台风中心风力不变，若城市受到的风力达到或超过四级，则称受台风影响．
    （1）该城市是否会受到这次台风的影响？为什么？
    （2）若受到台风影响，那么台风影响该城市的持续时间有多长？
    （3）该城市受到台风影响的最大风力为几级？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，抛物线y1=-x2+a与x轴正半轴交于点A，与y轴交于点B，点C（2，-3）在抛物线y1的图象上，连接AB，OC．
    （1）求抛物线y1的函数表达式；
    （2）若点P在x轴上，且∠CPA=∠OBA，求所有满足条件的点P的坐标；
    （3）将抛物线y1沿x轴向右平移后得抛物线y2，且抛物线y2的图象过点C．
    ①请直接写出抛物线y2的函数表达式；
    ②点Q在抛物线y2的图象上，且△OCQ是以OC为底边的等腰三角形，请直接写出所有符合条件的点Q的横坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，A港口某天受潮汐的影响，24小时内港口水深h（m）随时间t（时）的变化而变化．
    （1）水深h是时间t的函数吗？
    （2）当t分别取4，10，17时，h是多少？

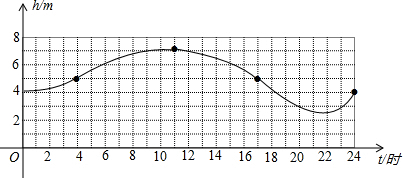
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．10张卡片分别写有11至20十个数字，将它们放入纸箱后，任意摸出一张，则P（摸到数字“13”）=$\frac{1}{10}$，P（摸到数字为偶数）=$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，在平面直角坐标系内，已知点A的位置；点B的坐标为（3，3）；点C的坐标为（5，1）．
    （1）写出A的坐标，并画出△ABC；
    （2）画出△ABC关于y轴对称的△A1B1C1；
    （3）求四边形AB B1A1的面积．

    查看答案和解析>>

    同步练习册答案