
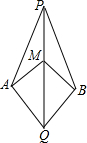
 如图,已知PA=PB,QA=QB,求证:MA=MB.
如图,已知PA=PB,QA=QB,求证:MA=MB. 分析 先证明△PQA≌△PQB得∠APQ=∠BPQ,再证明△PMA≌△PMB即可.
解答 证明: 在△PQA和△PQB中,
在△PQA和△PQB中,
$\left\{\begin{array}{l}{PQ=PQ}\\{PA=PB}\\{AQ=BQ}\end{array}\right.$,
∴△PQA≌△PQB,
∴∠APQ=∠BPQ,
在△PMA和△PMB中,
$\left\{\begin{array}{l}{PM=PM}\\{∠APM=∠BPM}\\{PA=PB}\end{array}\right.$,
∴△PMA≌△PMB,
∴AM=MB.
点评 本题考查全等三角形的判定和性质,解题的关键是两次利用全等三角形解决问题,证明全等时注意隐含条件公共边、公共角的应用,属于中考常考题型.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
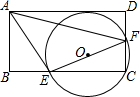 如图,矩形ABCD中,E为BC上一点,F为CD上一点,已知∠AEF=90°,$\frac{AE}{EF}$=$\frac{3}{4}$,△ECF的外接圆与AD相切,则tan∠DAF=$\frac{16}{63}$.
如图,矩形ABCD中,E为BC上一点,F为CD上一点,已知∠AEF=90°,$\frac{AE}{EF}$=$\frac{3}{4}$,△ECF的外接圆与AD相切,则tan∠DAF=$\frac{16}{63}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
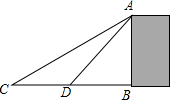 天下第一门-华门,位于山西省临汾市尧都区尧庙广场的西面,是一座纪念华夏文明的门.周日,小韬与同学一起来到华门前游玩,他想通过测量来计算华门的高度,于是他借来测角仪和卷尺,如图,他在点C处测得华门AB顶端A的仰角为30°,沿着CB方向向华门行进了36.6米到达点D处,测得华门AB顶端A的仰角为45°,求华门AB的高为多少?(结果保留整数,参考数据$\sqrt{3}$≈1.73)
天下第一门-华门,位于山西省临汾市尧都区尧庙广场的西面,是一座纪念华夏文明的门.周日,小韬与同学一起来到华门前游玩,他想通过测量来计算华门的高度,于是他借来测角仪和卷尺,如图,他在点C处测得华门AB顶端A的仰角为30°,沿着CB方向向华门行进了36.6米到达点D处,测得华门AB顶端A的仰角为45°,求华门AB的高为多少?(结果保留整数,参考数据$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
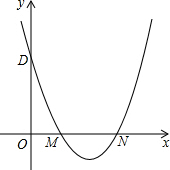 抛物线y=x2-4x+3交x轴于M,N点(M点在N点左边),交y轴于D点,点E为第一象限抛物线上的点,若∠EMN=2∠ODM,求E点坐标.
抛物线y=x2-4x+3交x轴于M,N点(M点在N点左边),交y轴于D点,点E为第一象限抛物线上的点,若∠EMN=2∠ODM,求E点坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com