
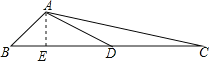
【题目】(1)如图,△ABC中,∠B=45°,AB=3![]() ,D是BC中点,tanC=
,D是BC中点,tanC=![]() .求BC的长与sin∠ADB.
.求BC的长与sin∠ADB.

(2)如图,在平面直角坐标系中,点A(0,4),B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,求直线BC的解析式.

【答案】(1) sin∠ADB =![]() ; (2) 直线BC的解析式为y=﹣
; (2) 直线BC的解析式为y=﹣![]() x+
x+![]() .
.
【解析】试题分析:(1) 过A作AE⊥BC于E,根据三角形函数分别求出AE、BE、CE的长,从而得BC的长,再由点D为BC中点即可得到DE的长, 根据勾股定理得AD长,从而得到∠ADB人正弦;
(2)在Rt△OAB中,OA=4,OB=3,用勾股定理计算出AB=5,再根据折叠的性质得BA′=BA=5,CA′=CA,则OA′=BA′-OB=2,设OC=t,则CA=CA′=4-t,在Rt△OA′C中,根据勾股定理得到求得t的值,从而确定出点C坐标,然后利用待定系数法确定直线BC的解析式.
试题解析:(1) 过A作AE⊥BC于E, ∴∠AEB=90°,
∵∠B=45°,∵sinB=![]() ,∴AE=ABsinB=3
,∴AE=ABsinB=3![]() ×
×![]() =3,∴BE=AE=3,
=3,∴BE=AE=3,
∵∠AEC=90°,tanC=![]() ,∴CE=15,∴BC=BE+CE=18;
,∴CE=15,∴BC=BE+CE=18;
∵D是BC中点,∴BD=![]() BC=9,∴DE=BD﹣BE=6,
BC=9,∴DE=BD﹣BE=6,
∴AD=![]() =3
=3![]() , ∴sin∠ADB=
, ∴sin∠ADB=![]() =
=![]() =
=![]() ;
;
(2)∵A(0,4),B(3,0),∴OA=4,OB=3,
在Rt△OAB中,AB=![]() =5,
=5,
∵△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,
∴BA′=BA=5,CA′=CA,∴OA′=BA′﹣OB=5﹣3=2,
设OC=t,则CA=CA′=4﹣t,在Rt△OA′C中,∵OC2+OA′2=CA′2,
∴t2+22=(4﹣t)2,解得t=![]() ,∴C点坐标为(0,
,∴C点坐标为(0, ![]() ),
),
设直线BC的解析式为y=kx+b,把B(3,0)、C(0, ![]() )代入得
)代入得 ,解得
,解得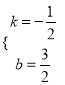 ,
,
∴直线BC的解析式为y=﹣![]() x+
x+![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在1、2、3、4、5这五个数中,先任意取一个数a,然后在余下的数中任意取出一个数b,组成一个点(a,b).求组成的点(a,b)恰好横坐标为偶数且纵坐标为奇数的概率.(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).
(1)求反比例函数的解析式;
(2)反比例函数的图象与线段BC交于点D,直线y=﹣![]() x+b过点D,与线段AB相交于点F,求点F的坐标;
x+b过点D,与线段AB相交于点F,求点F的坐标;
(3)连接OF、OE,探究∠AOF与∠EOC的数量关系,并证明;
(4)若点P是x轴上的动点,点Q是(1)中的反比例函数在第一象限图象上的动点,且使得△PDQ是以PQ为斜边的等腰直角三角形,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
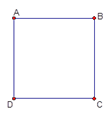
【题目】如图,四边形ABCD是一个正方形.
⑴请你在平面内找到一个点O,并连接OA、OB、OC、OD使得到△OAB、△BOC、△COD、△OAD都是等腰三角形.
⑵这样的点,你能找到多少个?
⑶试写出你找到的等腰三角形的顶角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饭店在2014年春节年夜饭的预定工作中,第一天预定了a桌,第二天预定的桌数比第一天多了4桌,则这两天该饭店一共预定了 桌年夜饭(用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=72°.
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com