练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    __________叫做一元二次方程ax2＋bx＋c＝0（a≠0）的根的判别式。通常用符号“Δ”来表示。

     

    答案：
    解析：

    		b2－4ac

     


    提示：

    		根的判别式是指Δ＝b2－4ac，而不是指Δ＝。

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    先阅读，再填空解答
    一元二次方程ax2+bx+c=o（a≠0）的求根公式是x=
    -b±
    		b2-4ac
    2a
    （b2-4ac≥0），显然这个一元二次方程的根的情况由b2-4ac来决定，我们把b2-4ac叫做一元二次方程ax2+bx+c=0的根的判别式，用符号“△”来表示．
    （1）当△＞0时，一元二次方程ax2+bx+c=0有两个
     
    根
    当△=0时，一元二次方程ax2+bx+c=0有两个
     
    根
    当△＜0时，一元二次方程ax2+bx+c=0
     
    根

    （2）已知关于x的方程，2x2-（4k+1）x+2k2-1=0，
    其中△=[-（4k+1）]2-4×2（2k2-1）=16k2+8k+1-16k2+8=8k+9
    ①当8k+9＞0时即k＞-
    9
    8
    时，原方程有两个不相等的实数根
    ②当8k+9=0时，即k=-
    9
    8
    时，原方程有两个相等的实数根
    ③当8k+9＜0时，即k＜-
    9
    8
    时，原方程没有实数根
    请根据阅读材料解答下面问题
    求证：关于x的方程x2-（2k+1）x+k-1=0有两个不相等的实数根．

    查看答案和解析>>

    科目：初中数学 来源：数学教研室 题型：022

    一元二次方程根的判别式___________叫做一元二次方程ax2＋bx＋c＝0（a≠0）的根的判别式，通常用符号“___________”表示．

    对于一元二次方程ax2＋bx＋c＝0（a≠0），当___________时，方程有两个不相等的实数根；当___________时，方程有两个相等的实数根；当___________时，方程没有实数根．反过来也成立．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    先阅读，再填空解答
    一元二次方程ax2+bx+c=o（a≠0）的求根公式是x=数学公式（b2-4ac≥0），显然这个一元二次方程的根的情况由b2-4ac来决定，我们把b2-4ac叫做一元二次方程ax2+bx+c=0的根的判别式，用符号“△”来表示．
    （1）当△＞0时，一元二次方程ax2+bx+c=0有两个______根
    当△=0时，一元二次方程ax2+bx+c=0有两个______根
    当△＜0时，一元二次方程ax2+bx+c=0______根

    （2）已知关于x的方程，2x2-（4k+1）x+2k2-1=0，
    其中△=[-（4k+1）]2-4×2（2k2-1）=16k2+8k+1-16k2+8=8k+9
    ①当8k+9＞0时即k＞-数学公式时，原方程有两个不相等的实数根
    ②当8k+9=0时，即k=-数学公式时，原方程有两个相等的实数根
    ③当8k+9＜0时，即k＜-数学公式时，原方程没有实数根
    请根据阅读材料解答下面问题
    求证：关于x的方程x2-（2k+1）x+k-1=0有两个不相等的实数根．

    查看答案和解析>>

    科目：初中数学 来源：2010年辽宁省营口市中考数学试卷（试测）（解析版） 题型：解答题

    先阅读，再填空解答
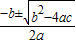    一元二次方程ax2+bx+c=o（a≠0）的求根公式是x=（b2-4ac≥0），显然这个一元二次方程的根的情况由b2-4ac来决定，我们把b2-4ac叫做一元二次方程ax2+bx+c=0的根的判别式，用符号“△”来表示．
    （1）当△＞0时，一元二次方程ax2+bx+c=0有两个______根
    当△=0时，一元二次方程ax2+bx+c=0有两个______根
    当△＜0时，一元二次方程ax2+bx+c=0______根

    （2）已知关于x的方程，2x2-（4k+1）x+2k2-1=0，
    其中△=[-（4k+1）]2-4×2（2k2-1）=16k2+8k+1-16k2+8=8k+9
    ①当8k+9＞0时即k＞-时，原方程有两个不相等的实数根
    ②当8k+9=0时，即k=-时，原方程有两个相等的实数根
    ③当8k+9＜0时，即k＜-时，原方程没有实数根
    请根据阅读材料解答下面问题
    求证：关于x的方程x2-（2k+1）x+k-1=0有两个不相等的实数根．

    查看答案和解析>>

    同步练习册答案