
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:解答题
| 用水量 | 单价 |
| x≤22 | a |
| 剩余部分 | a+1.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,OC平分∠AOD,OD平分∠BOC,下列结论不成立的是( )
如图,OC平分∠AOD,OD平分∠BOC,下列结论不成立的是( )| A. | ∠AOC=∠BOD | B. | ∠COD=$\frac{1}{2}$AOB | C. | ∠AOC=$\frac{1}{2}$∠AOD | D. | ∠BOC=2∠BOD |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a5+a5=a10 | B. | -a6•(-a)4=a10 | C. | (-bc)4÷(-bc)2=b2c2 | D. | (-ab)2•a=-a3b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
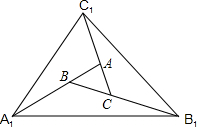 如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=AB,B1C=BC,C1A=CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1,B1C1,C1A1至A2,B2,C2,使得A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,记其面积为S2…,按此规律继续下去.第n次操作得到△AnBnCn,则S1=7,△AnBnCn的面积Sn=7n.
如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=AB,B1C=BC,C1A=CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1,B1C1,C1A1至A2,B2,C2,使得A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,记其面积为S2…,按此规律继续下去.第n次操作得到△AnBnCn,则S1=7,△AnBnCn的面积Sn=7n.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com