
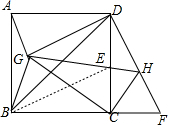
 如图,在边长为2$\sqrt{5}$的正方形ABCD中,点E是CD边的中点,延长BC至点F,使得CF=CE,连接BE,DF,将△BEC绕点C按顺时针方向旋转,当点E恰好落在DF上的点H处时,连接AG,DG,BG,则AG的长是2.
如图,在边长为2$\sqrt{5}$的正方形ABCD中,点E是CD边的中点,延长BC至点F,使得CF=CE,连接BE,DF,将△BEC绕点C按顺时针方向旋转,当点E恰好落在DF上的点H处时,连接AG,DG,BG,则AG的长是2. 分析 作辅助线,构建三角形高线,先利用勾股定理求DF的长,由三角函数得:FK=1,则CK=$\sqrt{(\sqrt{5})^{2}-1}$=2,
由等腰三角形三线合一得:HF=2,由面积法求得:HM=$\frac{4\sqrt{5}}{5}$,从而得:CM的长,设HM=4x,CM=3x,则CH=5x,由同角的三角函数列式:cos∠CGN=cos∠HCF=$\frac{3}{5}$=$\frac{GN}{CG}$,求出GN的长,依次求PG、AP的长,最后利用勾股定理得结论.
解答 解:如图,过C作CK⊥DF于K,过H作HM⊥CF于M,过G作PN⊥BC,交AD于P,交BC于N,
∵CD=2$\sqrt{5}$,CE=CF=$\sqrt{5}$,
∵四边形ABCD是正方形,
∴∠BCD=90°,
∴∠BCF=90°,
由勾股定理得:DF=$\sqrt{(\sqrt{5})^{2}+(2\sqrt{5})^{2}}$=5,
∵CK⊥DF,DC⊥CF,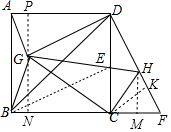
∴∠FCK=∠CDF,
sin∠FCK=sin∠CDF=$\frac{CF}{DF}=\frac{FK}{CF}$,
∴$\frac{\sqrt{5}}{5}=\frac{FK}{\sqrt{5}}$,
FK=1,
∴CK=$\sqrt{(\sqrt{5})^{2}-1}$=2,
由旋转得:CH=CE=CF,
∵CK⊥FH,
∴HF=KF=1,
∴HF=2,
∴S△CHF=$\frac{1}{2}$CF•HM=$\frac{1}{2}$HF•CK,
$\sqrt{5}$HM=2×2,
HM=$\frac{4\sqrt{5}}{5}$,
∴CM=$\sqrt{(\sqrt{5})^{2}-(\frac{4\sqrt{5}}{5})^{2}}$=$\frac{3\sqrt{5}}{5}$,
∴tan∠HCF=$\frac{HM}{CM}$=$\frac{\frac{4\sqrt{5}}{5}}{\frac{3\sqrt{5}}{5}}$=$\frac{4}{3}$,
设HM=4x,CM=3x,则CH=5x,
∵∠HCF=∠GCD=∠CGN,
∴cos∠CGN=cos∠HCF=$\frac{3}{5}$=$\frac{GN}{CG}$,
∴GN=$\frac{3}{5}$CG,
∵CG=BC=2$\sqrt{5}$,
∴GN=$\frac{3}{5}$×$2\sqrt{5}$=$\frac{6\sqrt{5}}{5}$,
∴NC=$\sqrt{C{G}^{2}-G{N}^{2}}$=$\sqrt{(2\sqrt{5})^{2}-(\frac{6\sqrt{5}}{5})^{2}}$=$\frac{8\sqrt{5}}{5}$,
∴GP=2$\sqrt{5}$-$\frac{6\sqrt{5}}{5}$=$\frac{4\sqrt{5}}{5}$,
∴AP=BN=BC-NC=2$\sqrt{5}$-$\frac{8\sqrt{5}}{5}$=$\frac{2\sqrt{5}}{5}$,
由勾股定理得:AG=$\sqrt{A{P}^{2}+G{P}^{2}}$=$\sqrt{(\frac{2\sqrt{5}}{5})^{2}+(\frac{4\sqrt{5}}{5})^{2}}$=2;
故答案为:2.
点评 本题考查了正方形的性质、勾股定理、三角函数、等腰三角形的性质,本题主要运用勾股定理和同角的三角函数求线段的长,同时还运用了面积法求线段的长,本题比较复杂,有难度.


科目:初中数学 来源: 题型:填空题
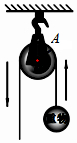 一个滑轮起重装置如图所示,滑轮的半径是10cm,当滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度为120°时,重物上升$\frac{20}{3}$πcm(结果保留π).
一个滑轮起重装置如图所示,滑轮的半径是10cm,当滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度为120°时,重物上升$\frac{20}{3}$πcm(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 组别 | 众数 | 中位数 | 平均数 |
| 甲 | 6 | 6 | 6.7 |
| 乙 | 8 | 7.5 | 7.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1的平方根是±1 | B. | 2是8的立方根 | ||
| C. | $\sqrt{2}$是2的一个平方根 | D. | -3是$\sqrt{9}$的平方根 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | A、B两点间的距离 | B. | A、C两点间的距离 | ||
| C. | A、B两点到原点的距离之和 | D. | A、C两点到原点的距离之和 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将⊙O沿弦AB折叠,圆弧AB恰好经过圆心O,P是$\widehat{AMB}$上一点,则∠APB的度数为( )
如图,将⊙O沿弦AB折叠,圆弧AB恰好经过圆心O,P是$\widehat{AMB}$上一点,则∠APB的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com