
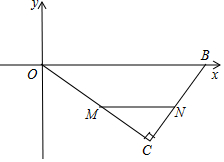
 已知:如图所示,在平面直角坐标系xOy中,∠C=90°,OB=25,OC=20,若点M是边OC上的一个动点(与点O、C不重合),过点M作MN∥OB交BC于点N.
已知:如图所示,在平面直角坐标系xOy中,∠C=90°,OB=25,OC=20,若点M是边OC上的一个动点(与点O、C不重合),过点M作MN∥OB交BC于点N.分析 (1)如图1,过C作CH⊥OB于H,根据勾股定理得到BC=$\sqrt{O{B}^{2}-O{C}^{2}}$=$\sqrt{2{5}^{2}-2{0}^{2}}$=15,根据三角形的面积公式得到CH=$\frac{OC•BC}{OB}$=$\frac{20×15}{25}$=12,由勾股定理得到OH=$\sqrt{O{C}^{2}-C{H}^{2}}$=16,于是得到结论;
(2)∵根据相似三角形的性质得到$\frac{CM}{CN}$=$\frac{OC}{BC}$=$\frac{20}{15}$=$\frac{4}{3}$,设CM=x,则CN=$\frac{3}{4}$x,根据已知条件列方程即可得到结论;
(3)如图2,由(2)知,当CM=x,则CN=$\frac{3}{4}$x,MN=$\frac{5}{4}$x,①当∠OMQ1=90°MN=MQ时,②当∠MNQ2=90°,MN=NQ2时,根据相似三角形的性质即可得到结论.
解答 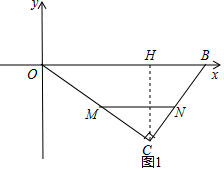 解:(1)如图1,过C作CH⊥OB于H,
解:(1)如图1,过C作CH⊥OB于H,
∵∠C=90°,OB=25,OC=20,
∴BC=$\sqrt{O{B}^{2}-O{C}^{2}}$=$\sqrt{2{5}^{2}-2{0}^{2}}$=15,
∵S△OBC=$\frac{1}{2}$OB•CH=$\frac{1}{2}$OC•BC,
∴CH=$\frac{OC•BC}{OB}$=$\frac{20×15}{25}$=12,
∴OH=$\sqrt{O{C}^{2}-C{H}^{2}}$=16,
∴C(16,-12);
(2)∵MN∥OB,
∴△CNM∽△COB,
∴$\frac{CM}{CN}$=$\frac{OC}{BC}$=$\frac{20}{15}$=$\frac{4}{3}$,
设CM=x,则CN=$\frac{3}{4}$x,
∵△MCN的周长与四边形OMNB的周长相等,
∴CM+CN+MN=OM+MN+OB,即x+$\frac{3}{4}$x+MN=20-x+mn+15-$\frac{3}{4}$x+25,
解得:x=$\frac{120}{7}$,
∴CM=$\frac{120}{7}$;
(3)如图2,由(2)知,当CM=x,则CN=$\frac{3}{4}$x,MN=$\frac{5}{4}$x,
①当∠OMQ1=90°MN=MQ时,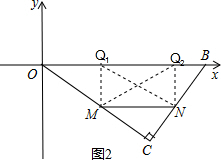
∵△OMQ∽△OBC,
∴$\frac{M{Q}_{1}}{BC}$=$\frac{OM}{OB}$,
∵MN=MQ,
∴$\frac{\frac{5}{4}x}{15}$=$\frac{20-x}{25}$,
∴x=$\frac{240}{37}$,
∴MN=$\frac{5}{4}$x=$\frac{5}{4}$×$\frac{240}{37}$=$\frac{300}{37}$;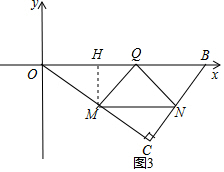
②当∠MNQ2=90°,MN=NQ2时,
此时,四边形MNQ2Q1是正方形,
∴NQ2=MQ1=MN,
∴MN=$\frac{300}{37}$.
③当∠MQN=90°,MQ=NQ时,
过M作MH⊥OB于H,∵MN=$\sqrt{2}$MQ,MQ=$\sqrt{2}$MH,∴MN=2MH,∴MH=$\frac{5}{8}$x,∵△OMH∽△OBC,∴$\frac{\frac{5}{8}x}{15}$=$\frac{20-x}{25}$,∴x=$\frac{480}{49}$,∴MN=$\frac{5}{4}$x=$\frac{600}{49}$.
点评 本题考查了相似三角形的判定和性质,正方形的判定和性质,勾股定理,三角形面积公式,正确的作出辅助线是解题的关键.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 负数有一个平方根 | |
| B. | $\frac{1}{4}$是0.5的一个平方根 | |
| C. | 72的平方根是7 | |
| D. | 正数有两个平方根,且这两个平方根之和等于0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | B. | 1,1,$\sqrt{3}$ | C. | 4,5,6 | D. | 1,$\sqrt{3}$,2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 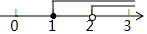 | B. | 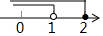 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 13cm | B. | 6cm | C. | 6cm或26cm | D. | 3cm或13cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com