
【题目】抛物线![]() 与
与![]() 轴交于A、B两点,点P在函数
轴交于A、B两点,点P在函数![]() 的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
A. 2个 B. 3个 C. 4个 D. 6个
【答案】D
【解析】分析:先由二次函数与一元二次方程的关系求出A、B两点的坐标,然后分类讨论:①当∠PAB=90°时,则P点的横坐标为-3,根据反比例函数图象上点的坐标特征易得P点有1个;②当∠APB=90°,设P(x,![]() ),根据两点间的距离公式和勾股定理可得(x+3)2+(
),根据两点间的距离公式和勾股定理可得(x+3)2+(![]() )2+(x-3)2+(
)2+(x-3)2+(![]() )2=36,此时P点有4个,③当∠PBA=90°时,P点的横坐标为3,此时P点有1个.
)2=36,此时P点有4个,③当∠PBA=90°时,P点的横坐标为3,此时P点有1个.
详解:解![]() 得,
得,
x=±3,
∴A(-3,0),B(3,0).
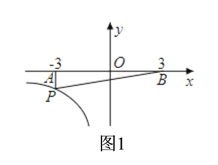
①当∠PAB=90°时,如图1,P点的横坐标为-3,把x=-3代入y=![]() 得y=-
得y=-![]() ,所以此时P点有1个;
,所以此时P点有1个;
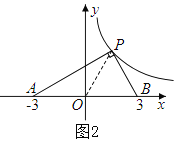
②当∠APB=90°,如图2,设P(x,![]() ),PA2=(x+3)2+(
),PA2=(x+3)2+(![]() )2,PB2=(x-3)2+(
)2,PB2=(x-3)2+(![]() )2,AB2=(3+3)2=36,
)2,AB2=(3+3)2=36,
∵PA2+PB2=AB2,
∴(x+3)2+(![]() )2+(x-3)2+(
)2+(x-3)2+(![]() )2=36,
)2=36,
整理得x4-9x2+4=0,所以x2=![]() ,或x2=
,或x2=![]() ,
,
所以此时P点有4个,
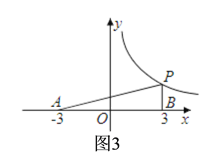
③当∠PBA=90°时,如图3,P点的横坐标为3,把x=3代入y=![]() 得y=
得y=![]() ,所以此时P点有1个;
,所以此时P点有1个;
综上所述,满足条件的P点有6个.
故选:D.


科目:初中数学 来源: 题型:
【题目】2019年12月14日,中国教育学会第32次学术年会在山东济南召开,某校选派16名教师前往参会,准备用一辆七座汽车(除司机外限载6人,从学校出发),送16位教师去高铁站与机场,其中11位教师准备一起到学校正东方向25千米处的机场,另外5位教师准备一起到学校正东方向15千米处的高铁站,其中去机场的老师中有6人因工作需要需先赶去机场,已知这辆汽车的平均速度为45千米/小时,教师步行的平均速度为5千米/小时.(注:不计教师上、下车时间,教师上车后,中途不下车,汽车到达目的地后立即沿原路返回)
(1)求汽车送第一批教师到达机场所用的时间.
(2)若只有这辆汽车送这16位教师去目的地后返回学校,请设计一种方案使该车所用总时间最短,并求出这个最短时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点A顺时针旋转得到△ADE(点B,C的对应点分别是D,E),当点E在BC边上时,连接BD,若∠ABC=30°,∠BDE=10°,求∠EAC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在甲批发市场以每包m元的价格进了40包茶叶,又在乙批发市场以每包n元![]() 的价格进了同样的60包茶叶,如果商家以每包
的价格进了同样的60包茶叶,如果商家以每包![]() 元的价格卖出这些茶叶,卖完后,这家商店( )
元的价格卖出这些茶叶,卖完后,这家商店( )
A. 盈利了B. 亏损了C. 不盈不亏D. 盈亏不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中xOy,抛物线y=x2-2(m-1)x+m2-4m+3的顶点为C,直线y=-2x+3与抛物线相交于A、B两点,点A在抛物线的对称轴的左侧.
(1)求点C的坐标(用含m的代数式表示);
(2)若P为直线OC上一动点,求△APB的面积;
(3)当OA+OB的值最小时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点O开始沿东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬行的各段路程依次为(单位:厘米):![]() .问:
.问:
(1)蜗牛最后是否回到出发点O?
(2)蜗牛离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则蜗牛可得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)
![]()
(1)数轴上点B对应的数是______.
(2)经过几秒,点M、点N分别到原点O的距离相等?
(3)当点M运动到什么位置时,恰好使AM=2BN?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.

根据以上信息解决下列问题:
(1)![]() ,
,![]() ;
;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 ![]() ;
;
(3)从选航模项目的![]() 名学生中随机选取
名学生中随机选取![]() 名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的
名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的![]() 名学生中恰好有
名学生中恰好有![]() 名男生、
名男生、![]() 名女生的概率.
名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一定数目的点或大小相同的圆在等距离的排列下可以形成一个等边三角形数阵.古希腊著名数学家毕达哥拉斯用数![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ……这些数量的(石子),都成功的排成了等边三角形数阵..
……这些数量的(石子),都成功的排成了等边三角形数阵..
(问题提出)![]() 结果等于多少?
结果等于多少?
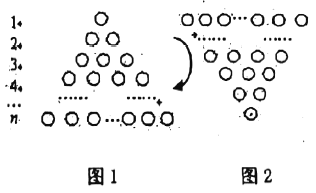
在图1所示的等边三角形数阵中,前![]() 行有
行有![]() 个圆圈,前
个圆圈,前![]() 行有
行有![]() 个圆圈,即
个圆圈,即![]() ,前
,前![]() 行有
行有![]() 个圆圈,即
个圆圈,即![]() ,…,则前
,…,则前![]() 行所有圆圈个数总和为
行所有圆圈个数总和为![]()
将图1旋转至图2,观察这两个三角形数阵中同一行圆圈个数(如第![]() 行的圆圈个数分别为
行的圆圈个数分别为![]() 个,
个,![]() 个),发现同一行圆圈个数之和均为___________个,由此可得两个图前
个),发现同一行圆圈个数之和均为___________个,由此可得两个图前![]() 行圆圈个数总和为:
行圆圈个数总和为:![]() ___________,因此,
___________,因此,![]() ___________.
___________.
(问题延伸)![]() 结果等于多少?
结果等于多少?
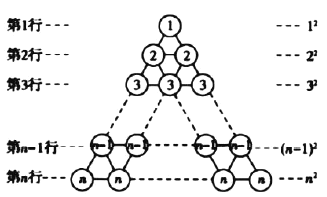
图3
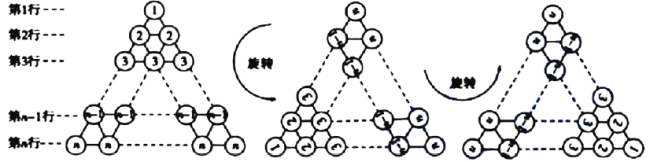
图4
在图3所示的等边三角形数阵中,第![]() 行圆圈中的数为
行圆圈中的数为![]() ,即
,即![]() ,第
,第![]() 行两个圆圈中数字的和为
行两个圆圈中数字的和为![]() .即
.即![]() …,第
…,第![]() 行
行![]() 个圆圈中数字的和为
个圆圈中数字的和为![]() (共
(共![]() 个).即
个).即![]() .这样,该三角形数阵中所有圆圈中数字的和为
.这样,该三角形数阵中所有圆圈中数字的和为![]() .
.
将该三角形数阵经两次旋转可得如图4所示的三个三角形数阵,观察这三个三角形数阵中各行同一位置上圆圈中的数字(如第![]() 行的第一个圆圈中的数字分别为
行的第一个圆圈中的数字分别为![]() ,
,![]() ,
,![]() ),发现相同位置上三个圆圈中数字之和均为___________,由此可得,这三个三角形数阵所有圆圈中数字的总和为:
),发现相同位置上三个圆圈中数字之和均为___________,由此可得,这三个三角形数阵所有圆圈中数字的总和为:![]() ___________,因此,
___________,因此,![]() ___________.
___________.
(规律应用)
根据以上发现,计算:![]() 的结果为___________.
的结果为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com