
【题目】“十一”黄金周的某一天,小王全家上午8时自驾小汽车从家里出发,到“番茄农庄”游玩,小汽车离家的距离![]() (千米)与小汽车离家后时间
(千米)与小汽车离家后时间![]() (时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题:
(时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题:

(1)“番茄农庄”离家________千米;
(2)小王全家在“番茄农庄”游玩了________小时;
(3)去时小汽车的平均速度是________千米/小时;
(4)回家时小汽车的平均速度是________千米/小时.
科目:初中数学 来源: 题型:
【题目】下列定理中,逆命题是假命题的是( )
A.等腰三角形的底角相等;
B.全等三角形的对应角相等;
C.直角三角形斜边上的中线等于斜边的一半;
D.线段垂直平分线上的任意一点到这条线段两个端点的距离相等。
查看答案和解析>>
科目:初中数学 来源: 题型:
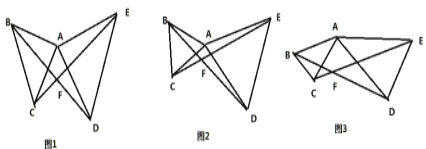
【题目】(1)如图 1,△ABC 和△ADE 都是等腰直角三角形,∠BAC 和∠DAE 是直角,连接BD,CE 相交于点 F,则∠BFC= °
(2)如图 2,△ABC 和△ADE 都是等边三角形,连接 BD,CE 相交于点 F,则∠BFC= °
(3)如图 3,△ABC 和△ADE 都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,连接 BD,CE相交于点 F,请猜想∠BFC 与∠BAC 有怎样的大小关系?请证明你的猜想
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0)、C(2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)设点M(3,n),求使MN+MD取最小值时n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣2,﹣1,0,1,2,3,4这7个数中任选一个数作为a的值,则使得关于x的分式方程![]() 有整数解,且关于x的一次函数y=(a+1)x+a﹣4的图象不经过第二象限的概率是 .
有整数解,且关于x的一次函数y=(a+1)x+a﹣4的图象不经过第二象限的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们已经学习了一元二次方程的解法,请从以下一元二次方程中任选两个,并选择你认为适当的方法解方程.
(1)3(x-1)2=48;
(2)3x2-7x+4=0;
(3)x(2x+3)=4x+6.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com