
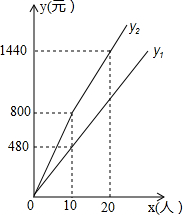
 某景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.
某景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.分析 (1)由函数图象,用购票款数除以定价的款数,得出a的值;用第11人到20人的购票款数除以定价的款数,得出b的值;
(2)利用待定系数法求正比例函数解析式求出y1,分x≤10与x>10,利用待定系数法求一次函数解析式求y2与x的函数关系式即可;
(3)设A团有n人,表示出B团的人数为(60-n),然后分0≤n≤10与n>10两种情况,根据(2)的函数关系式列出方程求解即可.
解答 解:(1)由y1图象上点(10,480),得到10人的费用为480元,
∴a=$\frac{480}{800}$×10=6;
由y2图象上点(10,800)和(20,1440),得到20人中后10人费用为640元,
∴b=$\frac{640}{800}$×10=8;
故答案为6,8.
(2)设y1=k1x,
∵函数图象经过点(0,0)和(10,480),
∴10k1=480,
∴k1=48,
∴y1=48x;
0≤x≤10时,设y2=k2x,
∵函数图象经过点(0,0)和(10,800),
∴10k2=800,
∴k2=80,
∴y2=80x,
x>10时,设y2=kx+b,
∵函数图象经过点(10,800)和(20,1440),
∴$\left\{\begin{array}{l}{10k+b=800}\\{20k+b=1440}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=64}\\{b=160}\end{array}\right.$,
∴y2=64x+160;
∴y2=$\left\{\begin{array}{l}{80x(0≤x≤10)}\\{64x+160(x>10)}\end{array}\right.$
(3)设A团有n人,则B团的人数为(60-n),
当0≤n≤10时,则B团的人数大于10人,
∴48n+64(60-n)+160=3360,
解得n=40(不符合题意舍去),
当n>10时,48n+64(60-n)+160=3360,
解得n=40,
则60-n=60-40=20.
答:A团有40人,B团有20人.
点评 此题是一次函数的应用,主要考查了待定系数法求函数解析式,方程的解法,图象的分析方法,解本题的关键是从图象上找到有用的点的坐标.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 王师傅开车通过福厦高速公路某隧道(全长约为7千米)时,所走路程为y(千米)与时间x(分钟)之间的函数关系的图象如图所示(A,B,C三点共线).王师傅说:“我开车通过隧道时,有一段连续2分钟恰好走了1.9千米”.你认为王师傅说有可能对吗?请说明理由.
王师傅开车通过福厦高速公路某隧道(全长约为7千米)时,所走路程为y(千米)与时间x(分钟)之间的函数关系的图象如图所示(A,B,C三点共线).王师傅说:“我开车通过隧道时,有一段连续2分钟恰好走了1.9千米”.你认为王师傅说有可能对吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
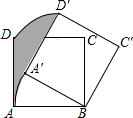 如图,正方形ABCD边长为3,将正方形ABCD绕点B顺时针旋转30°,得到正方形A′BC′D′,则图中阴影部分的面积是 $\frac{3}{4}π$.
如图,正方形ABCD边长为3,将正方形ABCD绕点B顺时针旋转30°,得到正方形A′BC′D′,则图中阴影部分的面积是 $\frac{3}{4}π$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
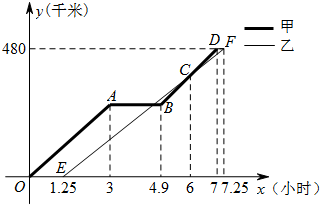 某市接到上级救灾的通知,派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
某市接到上级救灾的通知,派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com