
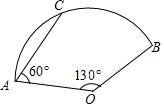
 如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则$\widehat{BC}$的长为$\frac{7}{3}$π.
如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则$\widehat{BC}$的长为$\frac{7}{3}$π. 分析 连接OC,如图,利用等腰三角形的性质和三角形内角和可计算出∠AOC=60°,则∠BOC=70°,然后根据弧长公式计算$\widehat{BC}$的长.
解答 解:连接OC,如图,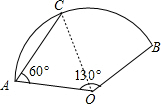
∵OA=OC,
∴∠OCA=∠CAO=60°,
∴∠AOC=60°,
∴∠BOC=130°-60°=70°,
∴$\widehat{BC}$的长=$\frac{70•π•6}{180}$=$\frac{7}{3}$π.
故答案为$\frac{7}{3}$π.
点评 本题考查了弧长的计算:圆周长公式:C=2πR;弧长公式:l=$\frac{n•π•R}{180}$(弧长为l,圆心角度数为n,圆的半径为R),在弧长的计算公式中,n是表示1°的圆心角的倍数,n和180都不要带单位.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,等边△OAB和等边△BCD的顶点A、C分别在双曲线y=$\frac{k}{x}$的图象上,若OA=1,则点C的坐标为($\frac{\sqrt{2}+1}{2}$,$\frac{\sqrt{6}-\sqrt{3}}{2}$).
如图,等边△OAB和等边△BCD的顶点A、C分别在双曲线y=$\frac{k}{x}$的图象上,若OA=1,则点C的坐标为($\frac{\sqrt{2}+1}{2}$,$\frac{\sqrt{6}-\sqrt{3}}{2}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com