
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一大重要研究成果.如图所示的三角形数表,称“杨辉三角”.具体法则:两侧的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律:
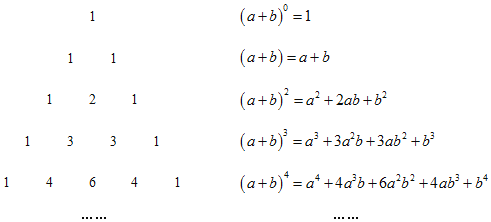
(1)根据上面的规律,写出(a+b)5的展开式;
(2)利用上面的规律计算:(﹣3)4+4×(﹣3)3×2+6×(﹣3)2×22+4×(﹣3)×23+24.
【答案】(1)(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;(2)1.
【解析】
(1)根据上面的规律,按a的次数由大到小的顺序判断出各是多少,写出(a+b)5的展开式即可;
(2)利用上面的规律,(-3)4+4×(-3)3×2+6×(-3)2×22+4×(-3)×23+24=(-3+2)4,据此求出算式的值是多少即可.
解:(1)根据规律可得:(a+b)5首项a的次数是5次方,b为0次方,后续每项a的次数减少1而b的次数增加1,每项的系数根据规律则依次为为1,1+4=5,4+6=10,6+4=10,4+1=5,1,根据以上规律,则(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
(2)由题知:![]() ,
,
对比(﹣3)4+4×(﹣3)3×2+6×(﹣3)2×22+4×(﹣3)×23+24
可知a=-3,b=2,
则原式=(﹣3+2)4=1.


科目:初中数学 来源: 题型:
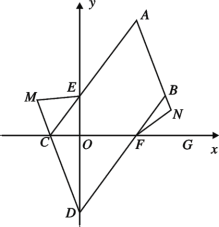
【题目】在平面直角坐标系中,点 A(a,6),B(4,b),
(1)若 a,b 满足 (a b 5)2 ![]() 0 ,
0 ,
①求点 A,B 的坐标;
②点 D 在第一象限,且点 D 在直线 AB 上,作 DC⊥x 轴于点 C,延长 DC 到 P 使 得 PC=DC,若△PAB 的面积为 10,求 P 点的坐标;
(2)如图,将线段 AB 平移到 CD,且点 C 在 x 轴负半轴上,点 D 在 y 轴负半轴上, 连接 AC 交 y 轴于点 E,连接 BD 交 x 轴于点 F,点 M 在 DC 延长线上,连 EM,3∠MEC+∠CEO=180°,点 N 在 AB 延长线上,点 G 在 OF 延长线上,∠NFG= 2∠NFB,请探究∠EMC 和∠BNF 的数量关系,给出结论并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
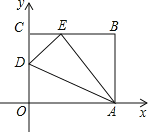
【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,则D点的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.

(1)探究:线段OE与OF的数量关系并加以证明;
(2)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明;若不是,则说明理由;
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算F,规定:F(x,y)=ax+by(其中a,b均为非零常数).例如:F(3,4)=3a+4b.
(1)已知F(1,﹣1)=﹣1,F(2,0)=4.
①求a,b的值;
②已知关于p的不等式组![]() ,求p的取值范围;
,求p的取值范围;
(2)若运算F满足![]() ,请你直接写出F(m,m)的取值范围(用含m的代数式表示,这里m为常数且m>0).
,请你直接写出F(m,m)的取值范围(用含m的代数式表示,这里m为常数且m>0).
查看答案和解析>>
科目:初中数学 来源: 题型:
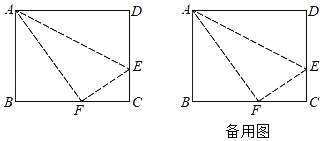
【题目】如图,长方形ABCD中,AB=8,BC=10,在边CD上取一点E,将△ADE折叠后点D恰好落在BC边上的点F处
(1)求CE的长;
(2)在(1)的条件下,BC边上是否存在一点P,使得PA+PE值最小?若存在,请求出最小值:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
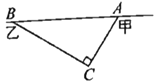
【题目】在甲村至乙村的公路上有一块山地正在开发,现有一![]() 处需要爆破.已知点
处需要爆破.已知点![]() 与公路上的停靠站
与公路上的停靠站![]() 的距离为300米,与公路上的另一停靠站
的距离为300米,与公路上的另一停靠站![]() 的距离为400米,且
的距离为400米,且![]() ,如图所示为了安全起见,爆破点
,如图所示为了安全起见,爆破点![]() 周围半径250米范围内不得进入,问在进行爆破时,公路
周围半径250米范围内不得进入,问在进行爆破时,公路![]() 段是否因为有危险而需要暂时封锁?请说明理由.
段是否因为有危险而需要暂时封锁?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.
(1)求证:AM=AC;
(2)若AC=3,求MC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com