
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() .
.

(1)求抛物线的解析式;
(2)点![]() 为第一象限抛物线上一点,连接
为第一象限抛物线上一点,连接![]() 、
、![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
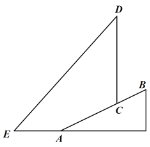
(3)在(2)的条件下,点![]() 为第四象限抛物线上一点,连接
为第四象限抛物线上一点,连接![]() ,过点
,过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() ,射线
,射线![]() 交第三象限抛物线于点
交第三象限抛物线于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)OB=2OC=4,则点B、C的坐标分别为(4,0)、(0,2),将点B、C坐标代入函数表达式![]() ,即可求解;
,即可求解;
(2)设PA交y轴于H,S△ACP=![]() ×CH×(xP-xA),先求出直线AP解析式,得出CH长,即可求解;
×CH×(xP-xA),先求出直线AP解析式,得出CH长,即可求解;
(3)当S=![]() 时,
时,![]() t2+
t2+![]() t=
t=![]() 得t=2,P(2,3),作EF⊥x轴,QM⊥x轴,CR⊥PM,EN⊥QR,
得t=2,P(2,3),作EF⊥x轴,QM⊥x轴,CR⊥PM,EN⊥QR,
tan∠EBF=![]() ,得DH=-m-1,∠QEB=2∠ABE,所以∠QEN=∠EBF,tan∠QEN=tan∠EBF,
,得DH=-m-1,∠QEB=2∠ABE,所以∠QEN=∠EBF,tan∠QEN=tan∠EBF,![]() ,得m=1-
,得m=1-![]() n,DK=-m+1,tan∠QCR=
n,DK=-m+1,tan∠QCR=![]() ,
,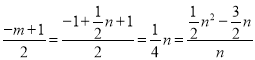 ,即可求解.
,即可求解.
(1)∵OB=2OC=4,
∴点B、C的坐标分别为(4,0)、(0,2),
将点B、C坐标代入函数表达式得:
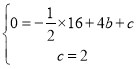
解得![]()
故函数的表达式为:![]()
故答案为:![]()
(2)设点P(t,![]() t2+
t2+![]() t+2),如图1,设PA交y轴于点H,
t+2),如图1,设PA交y轴于点H,

令![]()
解得x=-1或x=4
∴A(-1,0)
设直线AP解析式为y=kx+b
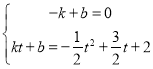
解得k=![]() (t4),b=
(t4),b=![]() (t4)
(t4)
∴直线AP解析式为:y=![]() (t4)x
(t4)x![]() (t4)
(t4)
令x=0,y=![]() (t4)
(t4)
∴CH=2+![]() (t4)=
(t4)=![]() t,
t,
S△ACP=![]() ×CH×(xPxA)=
×CH×(xPxA)=![]() ×
×![]() t×(t+1)=
t×(t+1)=![]() t2+
t2+![]() t,
t,
(3)当S=![]() 时,
时,![]() t2+
t2+![]() t=
t=![]()
得t=2,
∴P(2,3),
如图2,作EF⊥x轴,QM⊥x轴,CR⊥PM,EN⊥QR,
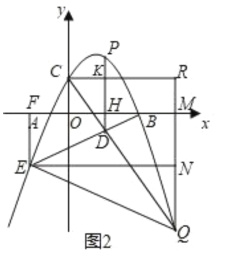
设E(m,![]() m2+
m2+![]() m+2),Q(n,
m+2),Q(n,![]() n2+
n2+![]() n+2),
n+2),
∵tan∠EBF=![]() ,
,
∴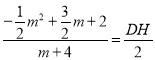
得DH=m1,
∵∠QEB=2∠ABE,
∴∠QEN=∠EBF
tan∠QEN=tan∠EBF, 即![]() ,
,
∴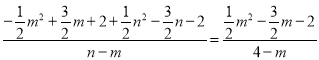
得m=1![]() n,
n,
DK=m+1,tan∠QCR=![]()
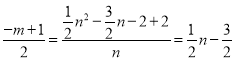
∴![]()
解得:n=6,
故点Q(6,7)
故答案为:Q(6,7)


科目:初中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)i=1:2.4的山坡AB上发现有一棵古树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为多少米?(参考数据:sin48°≈0.73,cos48°≈0.67,tan48°≈1.11)
查看答案和解析>>
科目:初中数学 来源: 题型:
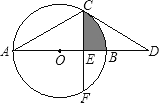
【题目】如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.
(1)求∠A的度数;
(2)若点F在⊙O上,CF⊥AB,垂足为E,CF=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学所在年级的500名学生参加志愿者活动,现有以下5个志愿服务项目:A,纪念馆志讲解员.B.书香社区图书整理C.学编中国结及义卖.D,家风讲解员E.校内志愿服务,要求:每位学生都从中选择一个项目参加,为了了解同学们选择这个5个项目的情况,该同学随机对年级中的40名同学选择的志愿服务项目进行了调查,过程如下:
收集数据:设计调查问卷,收集到如下数据(志愿服务项目的编号,用字母代号表示)
B,E,B,A,E,C,C,C,B,B,
A,C,E,D,B,A,B,E,C,A,
D,D,B,B,C,C,A,E,B
C,B,D,C,A,C,C,A,C,E,
(1)整理、描述诗句:划记、整理、描述样本数据,绘制统计图如下,请补全统计表和统计图

选择各志愿服务项目的人数统计表
志愿服务项目 | 划记 | 人数 |
A.纪念馆志愿讲解员 | 正 | 8 |
B.书香社区图书整理 | ||
C.学编中国结及义卖 | 正正 | 12 |
D.家风讲解员 | ||
E.校内志愿服务 | 正 一 | 6 |
合计 | 40 | 40 |
分析数据、推断结论
(2)抽样的40个样本数据(志愿服务项目的编号)的众数是 (填A﹣E的字母代号)
(3)请你任选A﹣E中的两个志愿服务项目,根据该同学的样本数据估计全年级大约有多少名同学选择这两个志愿服务项目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的正方形网格中,每个小正方形的边长均为1,
的正方形网格中,每个小正方形的边长均为1,![]() 的三个顶点均在小正方形的顶点上.
的三个顶点均在小正方形的顶点上.
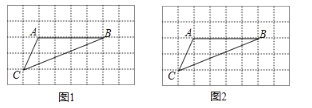
(1)在图1中画一个![]() (点
(点![]() 在小正方形的顶点上),使
在小正方形的顶点上),使![]() 的周长等于
的周长等于![]() 的周长,且以
的周长,且以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是轴对称图形;
为顶点的四边形是轴对称图形;
(2)在图2中画![]() (点
(点![]() 在小正方形的顶点上),使
在小正方形的顶点上),使![]() 的周长等于
的周长等于![]() 的周长,且以
的周长,且以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是中心对称图形;
为顶点的四边形是中心对称图形;
(3)直接写出图2中四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《小猪佩奇》这部动画片,估计同学们都非常喜欢.周末,小猪佩奇一家4口人(小猪佩奇,小猪乔治,小猪妈妈,小猪爸爸)到一家餐厅就餐,包厢有一圆桌,旁边有四个座位(![]() ,
,![]() ,
,![]() ,
,![]() ).
).


(1)小猪佩奇随机坐到![]() 座位的概率是________;
座位的概率是________;
(2)若现在由小猪佩奇,小猪乔治两人先后选座位,用树状图或列表的方法计算出小猪佩奇和小猪乔治坐对面的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 的直径
的直径![]() ,点
,点![]() 是
是![]() 延长线上的一点,过
延长线上的一点,过![]() 点作
点作![]() 的切线,切点为
的切线,切点为![]() ,连接
,连接![]() .
.

(1)若![]() ,求
,求![]() 的长;
的长;
(2)若点![]() 在
在![]() 的延长线上运动,
的延长线上运动,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,你认为
,你认为![]() 的大小是否发生变化?若变化,请说明理由;若不变化,求出
的大小是否发生变化?若变化,请说明理由;若不变化,求出![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调查某市市民上班时最常用的交通工具的情况,随机抽取了部分市民进行调查,要求被调查者从“![]() :自行车,
:自行车,![]() :家庭汽车,
:家庭汽车,![]() :公交车,
:公交车,![]() :电动车,
:电动车,![]() :其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
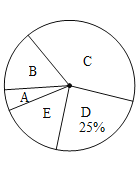
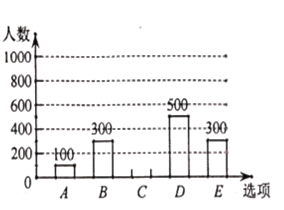
(1)本次调查中,一共调查了 名市民;扇形统计图中,![]() 项对应的扇形圆心角是_____
项对应的扇形圆心角是_____ ![]() ;
;
(2)补全条形统计图;
(3)若甲上班时从![]() 三种交通工具中随机选择一种, 乙上班时从
三种交通工具中随机选择一种, 乙上班时从![]() 三种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人都不选
三种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人都不选![]() 种交通工具上班的概率.
种交通工具上班的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com