
【题目】如图,在以线段AB为直径的⊙O上取一点,连接AC、BC.将△ABC沿AB翻折后得到△ABD.
(1)试说明点D在⊙O上;
(2)在线段AD的延长线上取一点E,使AB2=AC·AE.求证:BE为⊙O的切线;
(3)在(2)的条件下,分别延长线段AE、CB相交于点F,若BC=2,AC=4,求线段EF的长.
【答案】(1)证明见解析;(2)证明见解析;(3)EF=![]()
【解析】(1)由翻折知△ABC≌△ABD,得∠ADB=∠C=90°,据此即可得;
(2)由AB=AD知AB2=ADAE,即![]() ,据此可得△ABD∽△AEB,即可得出∠ABE=∠ADB=90°,从而得证;
,据此可得△ABD∽△AEB,即可得出∠ABE=∠ADB=90°,从而得证;
(3)由![]() 知DE=1、BE=
知DE=1、BE=![]() ,证△FBE∽△FAB得
,证△FBE∽△FAB得![]() ,据此知FB=2FE,在Rt△ACF中根据AF2=AC2+CF2可得关于EF的一元二次方程,解之可得.
,据此知FB=2FE,在Rt△ACF中根据AF2=AC2+CF2可得关于EF的一元二次方程,解之可得.
(1)∵AB为⊙O的直径,
∴∠C=90°,
∵将△ABC沿AB翻折后得到△ABD,
∴△ABC≌△ABD,
∴∠ADB=∠C=90°,
∴点D在以AB为直径的⊙O上;
(2)∵△ABC≌△ABD,
∴AC=AD,
∵AB2=ACAE,
∴AB2=ADAE,即![]() ,
,
∵∠BAD=∠EAB,
∴△ABD∽△AEB,
∴∠ABE=∠ADB=90°,
∵AB为⊙O的直径,
∴BE是⊙O的切线;
(3)∵AD=AC=4、BD=BC=2,∠ADB=90°,
∴AB=![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得:DE=1,
∴BE=![]() ,
,
∵四边形ACBD内接于⊙O,
∴∠FBD=∠FAC,即∠FBE+∠DBE=∠BAE+∠BAC,
又∵∠DBE+∠ABD=∠BAE+∠ABD=90°,
∴∠DBE=∠BAE,
∴∠FBE=∠BAC,
又∠BAC=∠BAD,
∴∠FBE=∠BAD,
∴△FBE∽△FAB,
∴![]() ,即
,即![]() ,
,
∴FB=2FE,
在Rt△ACF中,∵AF2=AC2+CF2,
∴(5+EF)2=42+(2+2EF)2,
整理,得:3EF2-2EF-5=0,
解得:EF=-1(舍)或EF=![]() ,
,
∴EF=![]() .
.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】小亮从家出发步行到公交站台后,等公交车去学校,如图, 折线表示这个过程中行程 s (千米)与所花时间 t (分)之间的关系,下 列说法错误的是( )
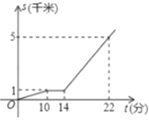
A.他家到公交车站台需行 1 千米B.他等公交车的时间为 4 分钟
C.公交车的速度是 500 米/分D.他步行与乘公交车行驶的平均速度300米/分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
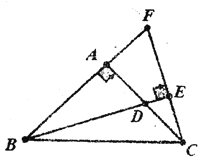
【题目】如图,等腰直角三角形ABC中,∠BAC=90°,D是AC的中点,EC⊥BD于E,交BA的延长线于F,若BF=12,则△BDC的面积是______
查看答案和解析>>
科目:初中数学 来源: 题型:
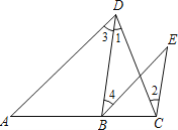
【题目】已知:如图,∠1=∠2,∠3=∠E,试说明:∠A=∠EBC,(请按图填空,并补理由,)
证明:∵∠1=∠2(已知),
∴______∥______,________
∴∠E=∠______,________
又∵∠E=∠3(已知),
∴∠3=∠______(等量代换),
∴______∥______(内错角相等,两直线平行),
∴∠A=∠EBC,________
查看答案和解析>>
科目:初中数学 来源: 题型:
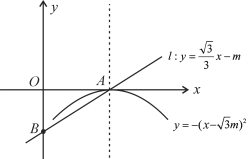
【题目】如图所示,抛物线![]() (m>0)的顶点为A,直线
(m>0)的顶点为A,直线![]() 与
与![]() 轴的交点为点B.
轴的交点为点B.
(1)求出抛物线的对称轴及顶点A的坐标(用含![]() 的代数式表示);
的代数式表示);
(2)证明点A在直线![]() 上,并求∠OAB的度数;
上,并求∠OAB的度数;
(3)动点Q在抛物线对称轴上,问:抛物线上是否存在点P,使以点P、Q、A为顶点的三角形与△OAB全等?若存在,求出![]() 的值,并写出所有符合上述条件的点P的坐标;若不存在,请说明理由.
的值,并写出所有符合上述条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
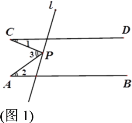
【题目】已知直线AB∥CD,点P为直线l上一点,尝试探究并解答:
(1)如图1,若点P在两平行线之间,∠1=23°,∠2=35°,则∠3= ;
(2)探究图1中∠1,∠2与∠3之间的数量关系,并说明理由;
(3)如图2,若点P在CD的上方,探究∠1,∠2与∠3之间有怎样的数量关系,并说明理由;
(4)如图3,若∠PCD与∠PAB的平分线交于点P1,∠DCP1与∠BAP1的平分线交于点P2,∠DCP2与∠BAP2的平分线交于点P3,…,∠DCPn-1与∠BAPn-1的平分线交于点Pn,若∠PCD=α,∠PAB=β,直接写出∠APnC的度数(用含α与β的代数式表示).


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.

(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
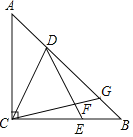
【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别在边AB、CB上,CD=DE,∠CDB=∠DEC,过点C作CF⊥DE于点F,交AB于点G,
(1)求证:△ACD≌△BDE;
(2)求证:△CDG为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点是
的顶点是![]() ,抛物线
,抛物线![]() 的顶点是
的顶点是![]() .
.
(1)判断点![]() 是否在抛物线
是否在抛物线![]() 上,为什么?
上,为什么?
(2)如果抛物线![]() 经过点
经过点![]() .
.
①求![]() 的值;
的值;
②直线![]() 与
与![]() 分别交于点
分别交于点![]() (点
(点![]() 在
在![]() 的左边),直线
的左边),直线![]() 与
与![]() 分别交于点
分别交于点![]() (点
(点![]() 在
在![]() 的左边)是否存在
的左边)是否存在![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 值;若不存在,说明理由.
值;若不存在,说明理由.
③在②的条件下,当![]() 为何值时, 抛物线
为何值时, 抛物线![]() 和
和![]() 中
中![]() 都随
都随![]() 的增大而增大?
的增大而增大?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com