
 ЕФХзЮяЯпОЙ§ЕуAЃЈ6ЃЌ0ЃЉКЭBЃЈ0ЃЌ4ЃЉЃЎ
ЕФХзЮяЯпОЙ§ЕуAЃЈ6ЃЌ0ЃЉКЭBЃЈ0ЃЌ4ЃЉЃЎ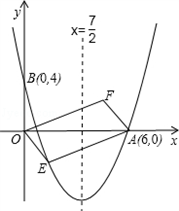
 ЃЌ
ЃЌ ЃЉ2+kЃЎ
ЃЉ2+kЃЎ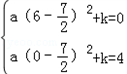 ЃЌ
ЃЌ ЃЌk=Љ
ЃЌk=Љ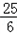 ЃЎ
ЃЎ ЃЈxЉ
ЃЈxЉ ЃЉ2Љ
ЃЉ2Љ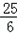 ЃЌЖЅЕуЮЊЃЈ
ЃЌЖЅЕуЮЊЃЈ ЃЌЉ
ЃЌЉ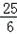 ЃЉЃЛ
ЃЉЃЛ ЃЈxЉ
ЃЈxЉ ЃЉ2=
ЃЉ2=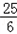 ЃЌ
ЃЌ ЁСOAЁЄ|y|=Љ6y=Љ4ЃЈxЉ
ЁСOAЁЄ|y|=Љ6y=Љ4ЃЈxЉ ЃЉ2+25ЃЎ
ЃЉ2+25ЃЎ ЃЉ2+25=24ЃЎ
ЃЉ2+25=24ЃЎ ЃЉ2=
ЃЉ2= ЃЎ
ЃЎ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
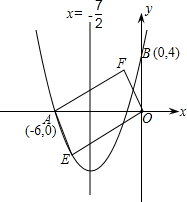 ЃЈ2013•мьФЯЯиЖўФЃЃЉШчЭМЃЌЖдГЦжсЮЊжБЯпx=-
ЃЈ2013•мьФЯЯиЖўФЃЃЉШчЭМЃЌЖдГЦжсЮЊжБЯпx=-| 7 | 2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
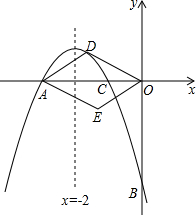 ШчЭМЃЌЖдГЦжсЮЊжБЯпx=-2ЕФХзЮяЯпОЙ§AЃЈ-3ЃЌ0ЃЉКЭBЃЈ0ЃЌ-3ЃЉЃЎ
ШчЭМЃЌЖдГЦжсЮЊжБЯпx=-2ЕФХзЮяЯпОЙ§AЃЈ-3ЃЌ0ЃЉКЭBЃЈ0ЃЌ-3ЃЉЃЎ| 9 | 4 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ШчЭМЃЌЖдГЦжсЮЊжБЯпx=
ШчЭМЃЌЖдГЦжсЮЊжБЯпx=| 7 | 2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
| 7 | 2 |
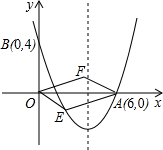 ааЫФБпаЮЃПШєФмЃЌЧѓГіЕуEЁЂFЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎЃЈЕкЃЈ4ЃЉЮЪВЛаДНтД№Й§ГЬЃЌжЛаДНсТлЃЉ
ааЫФБпаЮЃПШєФмЃЌЧѓГіЕуEЁЂFЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎЃЈЕкЃЈ4ЃЉЮЪВЛаДНтД№Й§ГЬЃЌжЛаДНсТлЃЉВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 вбжЊШчЭМЃЌЖдГЦжсЮЊжБЯпx=4ЕФХзЮяЯпy=ax2+2xгыxжсЯрНЛгкЕуBЁЂOЃЎ
вбжЊШчЭМЃЌЖдГЦжсЮЊжБЯпx=4ЕФХзЮяЯпy=ax2+2xгыxжсЯрНЛгкЕуBЁЂOЃЎВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com