

分析 (1)根据平行线的判定与性质填写即可;
(2)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案;
(3)画出图形(分两种情况①点P在BA的延长线上,②点P在AB的延长线上),根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案.
解答  解:(1)过点P作PE∥AB,
解:(1)过点P作PE∥AB,
如图2所示:
∵AB∥CD,
∴PE∥CD.(平行于同一条直线的两条直线平行)
∴∠A+∠APE=180°.
∠C+∠CPE=180°.(两直线平行同旁内角互补)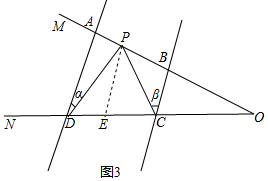
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.(等量代换)
故答案为:平行于同一条直线的两条直线平行;两直线平行,同旁内角互补;等量代换;
(2)∠CPD=∠α+∠β,理由如下:
如图3所示,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
(3)当P在BA延长线时,如图4所示:
过P作PE∥AD交CD于E,
同(2)可知:∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠β-∠α;
当P在AB延长线时,如图5所示:
同(2)可知:∠α=∠DPE,∠β=∠CPE,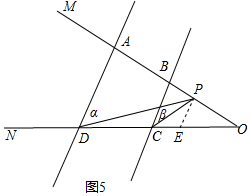
∴∠CPD=∠α-∠β.
点评 本题考查了平行线的性质和判定的应用,主要考查学生的推理能力,题目是一道比较典型的题目,有一定难度.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:选择题
| A. | 若a+b=0,则$\frac{a}{b}$=-1 | B. | 若|a|=-a,则a<0 | ||
| C. | 若a>b>0,则-a<-b<0 | D. | 若a<b<0,则$\frac{1}{a}$<$\frac{1}{b}$<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,那么,我们称抛物线C1与C2关联.
如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,那么,我们称抛物线C1与C2关联.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
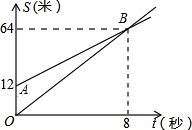 如图,OB,AB分别表示甲乙两名同学运动的一次函数图象,图中s与t分别表示运动路程和时间,已知甲的速度比乙快,下列说法:
如图,OB,AB分别表示甲乙两名同学运动的一次函数图象,图中s与t分别表示运动路程和时间,已知甲的速度比乙快,下列说法:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
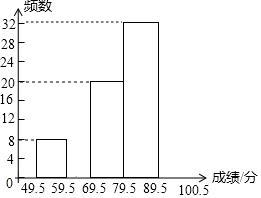 6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频数分布表和不完整的频数分布直方图如下:
6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频数分布表和不完整的频数分布直方图如下:| 分组 | 频数 | 所占百分比 |
| 49.5~59.5 | 8 | 8% |
| 59.5~69.5 | 12 | 12% |
| 69.5~79.5 | 20 | 20% |
| 79.5~89.5 | 32 | 32% |
| 89.5~100.5 | 28 | a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
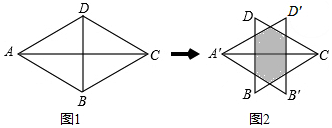
| A. | ① | B. | ①② | C. | ①③ | D. | ①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com