
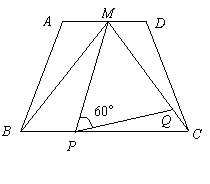
如图13,在梯形![]() 中,
中,![]() 点
点![]() 是
是![]() 的中点,
的中点,![]() 是等边三角形.
是等边三角形.
(1)求证:梯形![]() 是等腰梯形;
是等腰梯形;
(2)动点![]() 、
、![]() 分别在线段
分别在线段![]() 和
和![]() 上运动,且
上运动,且![]() 保持不变.设
保持不变.设![]() 求
求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)在(2)中:①当动点![]() 、
、![]() 运动到何处时,以点
运动到何处时,以点![]() 、
、![]() 和点
和点![]() 、
、![]() 、
、![]() 、
、![]() 中的两个点为顶点的四边形是平行四边形?并指出符合条件的平行四边形的个数;
中的两个点为顶点的四边形是平行四边形?并指出符合条件的平行四边形的个数;
②当![]() 取最小值时,判断
取最小值时,判断![]() 的形状,并说明理由.
的形状,并说明理由.
 |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 2×1 |
| 1 |
| 3 |
3×
|
| 8×8 |
| ab |
| a |
| b |
| ab |
| ab |
| ab |
查看答案和解析>>
科目:初中数学 来源: 题型:
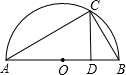
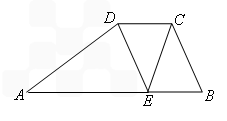
 (2012•嘉定区二模)如图,已知梯形ABCD中,AB∥CD,AB=13,CD=4,点E在边AB上,DE∥BC.
(2012•嘉定区二模)如图,已知梯形ABCD中,AB∥CD,AB=13,CD=4,点E在边AB上,DE∥BC.查看答案和解析>>
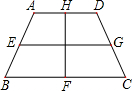
科目:初中数学 来源:上海市期中题 题型:解答题
 中,AB∥CD,AB=13,CD=4,点
中,AB∥CD,AB=13,CD=4,点 在边AB上,DE∥
在边AB上,DE∥ 。
。
 ,且
,且 ,求
,求 的面积;
的面积;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com