

分析 (1)根据矩形的性质找出∠B=∠C=90°,再通过角的计算得出∠BAP=∠CPD,由此即可得出△ABP∽△PCD;
(2)过点F作FH⊥PC于点H,根据矩形的性质以及角的计算找出∠B=∠FHP=90°、∠BEP=∠HPF,由此即可得出△BEP∽△HPF,根据相似三角形的性质,找出边与边之间的关系即可得出结论;
(3)分点E在AB和AD上两种情况考虑,根据相似三角形的性质找出各边的长度,再利用分割图形求面积法找出S与t之间的函数关系式,令S=4.2求出t值,此题得解.
解答 解:(1)∵四边形ABCD为矩形,
∴∠B=∠C=90°,
∴∠BAP+∠BPA=90°.
∵∠MPN=90°,
∴∠BPA+∠CPD=90°,
∴∠BAP=∠CPD,
∴△ABP∽△PCD.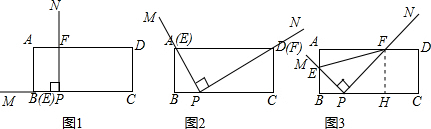
故答案为:∽.
(2)是定值.如图3,过点F作FH⊥PC于点H,
∵矩形ABCD中,AB=2,
∴∠B=∠FHP=90°,HF=AB=2,
∴∠BPE+∠BEP=90°.
∵∠MPN=90°,
∴∠BPE+∠HPE=90°,
∴∠BEP=∠HPF,
∴△BEP∽△HPF,
∴$\frac{PE}{PF}=\frac{BP}{HF}$,
∵BP=1,
∴$\frac{PE}{PF}=\frac{1}{2}$.
(3)分两种情况:
①如图3,当点E在AB上时,0≤t≤2.
∵AE=t,AB=2,
∴BE=2-t.
由(2)可知:△BEP∽△HPE,
∴$\frac{BE}{HP}=\frac{PE}{PF}$,即$\frac{2-t}{HP}=\frac{1}{2}$,
∴HP=4-2t.
∵AF=BH=PB+BH=5-2t,
∴S=S矩形ABHF-S△AEF-S△BEP-S△PHF=AB•AF-$\frac{1}{2}$AE•AF-$\frac{1}{2}$BE•PB-$\frac{1}{2}$PH•FH=t2-4t+5(0≤t≤2).
当S=4.2时,t2-4t+5=4.2,
解得:t=2±$\frac{4}{5}\sqrt{5}$.
∵0≤t≤2,
∴t=2-$\frac{4}{5}\sqrt{5}$;
②如图4,当点E在AD上时,0≤t≤1,过点E作EK⊥BP于点K,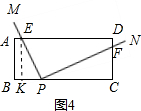
∵AE=t,BP=1,
∴PK=1-t.
同理可证:△PKE∽△FCP,
∴$\frac{PK}{FC}=\frac{PE}{PF}$,即$\frac{1-t}{FC}=\frac{1}{2}$,
∴FC=2-2t.
∴DF=CD-FC=2t,DE=AD-AE=5-t,
∴S=S矩形EKCD-S△EKP-S△EDF-S△PCF=CD•DE-$\frac{1}{2}$EK•KP-$\frac{1}{2}$DE•DF-$\frac{1}{2}$PC•FC=t2-2t+5(0≤t≤1).
当S=4.2时,t2-2t+5=4.2,
解得:t=1±$\frac{\sqrt{5}}{5}$.
∵0≤t≤1,
∴t=1-$\frac{\sqrt{5}}{5}$.
综上所述:当点E在AB上时,S=t2-4t+5(0≤t≤2),当S=4.2时,t=2-$\frac{4}{5}\sqrt{5}$;当点E在AD上时,S=t2-2t+5(0≤t≤1),当S=4.2时,t=1-$\frac{\sqrt{5}}{5}$.
点评 本题考查了矩形的性质、相似三角形的判定与性质以及三角形的面积,解题的关键是:(1)熟练掌握相似三角形的判定定理;(2)根据相似三角形的性质找出$\frac{PE}{PF}=\frac{BP}{HF}$;(3)分点E在AB和AD上两种情况考虑.本题属于中档题,难度不大,解决该题型题目时,根据相似三角形的性质找出边与边之间的关系是关键.


科目:初中数学 来源: 题型:选择题
 如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中一定成立的等量关系是( )
如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中一定成立的等量关系是( )| A. | S矩形AMKP=S矩形KQCN | |
| B. | S${\;}_{矩{形}_{MBQK}}$>S矩形PKND | |
| C. | S矩形AMKP>S矩形KQCN | |
| D. | S矩形AMKP+S矩形KQCN=S矩形MBQK+S矩形PKND |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2(x+y)(x-y) | B. | 4(x+y)(x-y) | C. | (x+y)(x-y) | D. | 4(x+y)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠C=90°,将△ABC绕点B顺时针旋转,得到△A′BC′,点C′在AB的延长线上,连接AA′,若∠AA′B=35°,则∠CAB的度数是( )
如图,在Rt△ABC中,∠C=90°,将△ABC绕点B顺时针旋转,得到△A′BC′,点C′在AB的延长线上,连接AA′,若∠AA′B=35°,则∠CAB的度数是( )| A. | 10° | B. | 15° | C. | 20° | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=1,b=2 | B. | a=2,b=3 | C. | a=3,b=4 | D. | a=4,b=5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com