
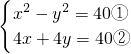 ,
,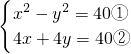 ,则由①变形(x+y)(x-y)=40③,由②得x+y=10④,
,则由①变形(x+y)(x-y)=40③,由②得x+y=10④,

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:同步轻松练习 九年级 数学 上 题型:013
小明要在一幅长90厘米、宽40厘米的水彩画的外围,镶上一条宽度相等的金色彩条,要求使水彩画的面积是整幅画面积的54%,设金色彩条的宽为x厘米,根据题意列方程为
A.(90+x)(40+x)×54%=90×40
B.(90+2x)(40+2x)×54%=90×40
C.(90+x)(40+2x)×54%=90×40
D.(90+2x)(40+x)×54%=90×40
查看答案和解析>>
科目:初中数学 来源:解题升级解题快速反应一典通八年级数学 题型:044
将一条20cm长的金彩带剪成两段,恰好用来镶两张大小不同的正方形壁画的边(不计接头处),已知两张壁画的面积相差20cm2,问能否剪成?若能,请问该如何剪?若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com