
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F. 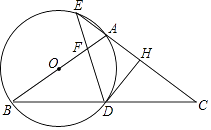
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求 ![]() 的值;
的值;
(3)若EA=EF=1,求圆O的半径.
【答案】
(1)证明:连接OD,如图1,
∵OB=OD,
∴△ODB是等腰三角形,
∠OBD=∠ODB①,
在△ABC中,∵AB=AC,
∴∠ABC=∠ACB②,
由①②得:∠ODB=∠OBD=∠ACB,
∴OD∥AC,
∵DH⊥AC,
∴DH⊥OD,
∴DH是圆O的切线

(2)解:如图2,在⊙O中,∵∠E=∠B,
∴由(1)可知:∠E=∠B=∠C,
∴△EDC是等腰三角形,
∵DH⊥AC,且点A是EH中点,
设AE=x,EC=4x,则AC=3x,
连接AD,则在⊙O中,∠ADB=90°,AD⊥BD,
∵AB=AC,
∴D是BC的中点,
∴OD是△ABC的中位线,
∴OD∥AC,OD= ![]() AC=
AC= ![]() ×3x=
×3x= ![]() ,
,
∵OD∥AC,
∴∠E=∠ODF,
在△AEF和△ODF中,
∵∠E=∠ODF,∠OFD=∠AFE,
∴△AEF∽△ODF,
∴ ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]()

(3)解:如图2,设⊙O的半径为r,即OD=OB=r,
∵EF=EA,
∴∠EFA=∠EAF,
∵OD∥EC,
∴∠FOD=∠EAF,
则∠FOD=∠EAF=∠EFA=∠OFD,
∴DF=OD=r,
∴DE=DF+EF=r+1,
∴BD=CD=DE=r+1,
在⊙O中,∵∠BDE=∠EAB,
∴∠BFD=∠EFA=∠EAB=∠BDE,
∴BF=BD,△BDF是等腰三角形,
∴BF=BD=r+1,
∴AF=AB﹣BF=2OB﹣BF=2r﹣(1+r)=r﹣1,
在△BFD和△EFA中,
∵ ![]() ,
,
∴△BFD∽△EFA,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:r1= ![]() ,r2=
,r2= ![]() (舍),
(舍),
综上所述,⊙O的半径为 ![]()
【解析】(1)根据同圆的半径相等和等边对等角证明:∠ODB=∠OBD=∠ACB,则DH⊥OD,DH是圆O的切线;(2)如图2,先证明∠E=∠B=∠C,则H是EC的中点,设AE=x,EC=4x,则AC=3x,由OD是△ABC的中位线,得:OD= ![]() AC=
AC= ![]() ,证明△AEF∽△ODF,列比例式可得结论;(3)如图2,设⊙O的半径为r,即OD=OB=r,证明DF=OD=r,则DE=DF+EF=r+1,BD=CD=DE=r+1,证明△BFD∽△EFA,列比例式为:
,证明△AEF∽△ODF,列比例式可得结论;(3)如图2,设⊙O的半径为r,即OD=OB=r,证明DF=OD=r,则DE=DF+EF=r+1,BD=CD=DE=r+1,证明△BFD∽△EFA,列比例式为: ![]() ,则
,则 ![]() =
= ![]() ,求出r的值即可.
,求出r的值即可.


科目:初中数学 来源: 题型:
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
查看答案和解析>>
科目:初中数学 来源: 题型:
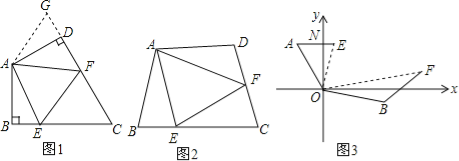
【题目】(13分)(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得线段BE、EF、FD之间的数量关系为 .
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF=![]() ∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
(3)如图3,点A在点O的北偏西30°处,点B在点O的南偏东70°处,且AO=BO,点A沿正东方向移动249米到达E处,点B沿北偏东50°方向移动334米到达点F处,从点O观测到E、F之间的夹角为70°,根据(2)的结论求E、F之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
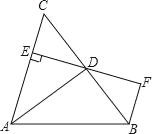
A. ①②③④ B. ①②④ C. ①②③ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.

(1)点D在边AB上时,试探究线段BD、AB和AF的数量关系,并证明你的结论;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请直接写出正确结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
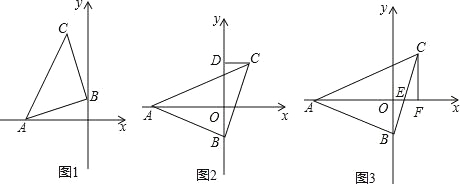
【题目】已知,△ABC 是等腰直角三角形,BC=AB,A 点在 x 负半轴上,直角顶点 B 在 y 轴上,点 C 在 x 轴上方.
(1)如图1所示,若A的坐标是(﹣3,0),点 B的坐标是(0,1),求点 C 的坐标;
(2)如图2,过点 C 作 CD⊥y 轴于 D,请直接写出线段OA,OD,CD之间等量关系;
(3)如图3,若 x 轴恰好平分∠BAC,BC与 x 轴交于点 E,过点 C作 CF⊥x 轴于 F,问 CF 与 AE 有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及平行四边形ABDC的面积![]() .
.
(2)在y轴上是否存在一点P,连接PA,PB,使![]() =2
=2![]() ,若存在这样一点,求出点P的坐标,若不存在,试说明理由.
,若存在这样一点,求出点P的坐标,若不存在,试说明理由.
(3)点P是四边形ABCD边上的点,若△OPC为等腰三角形时,直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
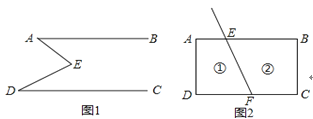
【题目】如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③猜想图1中∠AED,∠EAB,∠EDC的关系并证明你的结论.
(2)拓展应用:如图2,线段FE与长方形ABCD的边AB交于点E,与边CD 交于点F.图2中①②分别是被线段FE隔开的2个区域(不含边界),P是位于以上两个区域内的一点,猜想∠PEB,∠PFC,∠EPF的关系(不要求说明理由).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com