
”¾ĢāÄæ”æĪŖĮĖĒŠŹµ¹Ų×¢”¢¹Ų°®Ę¶Ą§¼ŅĶ„ѧɜ£¬Ä³Š£¶ŌČ«Š£ø÷°ąĘ¶Ą§¼ŅĶ„ѧɜµÄČĖŹżĒéæö½ųŠŠĮĖĶ³¼Ę£¬ŅŌ±ć¹ś¼Ņ¾«×¼·öĘ¶Õž²ßÓŠŠ§Ā䏵£®Ķ³¼Ę·¢ĻÖ°ąÉĻʶĄ§¼ŅĶ„ѧɜČĖŹż·Ö±šÓŠ2Ćū”¢3Ćū”¢4Ćū”¢5Ćū”¢6Ćū£¬¹²ĪåÖÖĒéæö£®²¢½«ĘäÖĘ³ÉĮĖČēĻĀĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£ŗ 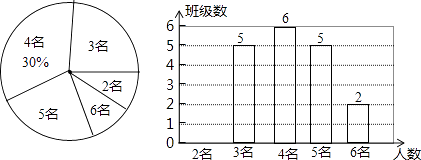
£Ø1£©ĒóøĆŠ£Ņ»¹²ÓŠ¶ąÉŁøö°ą£æ²¢½«ĢõŠĪĶ¼²¹³äĶźÕū£»
£Ø2£©Ä³°®ŠÄČĖŹæ¾ö¶Ø“Ó2ĆūʶĄ§¼ŅĶ„ѧɜµÄÕāŠ©°ą¼¶ÖŠ£¬ČĪŃ”Į½Ćū½ųŠŠ°ļ·ö£¬ĒėÓĆĮŠ±ķ·Ø»ņŹ÷דĶ¼µÄ·½·Ø£¬Ēó³ö±»Ń”ÖŠµÄĮ½ĆūѧɜĄ“×ŌĶ¬Ņ»°ą¼¶µÄøÅĀŹ£®
”¾“š°ø”æ
£Ø1£©½ā£ŗøĆŠ£µÄ°ą¼¶¹²ÓŠ6”Ā30%=20£Øøö£©£¬
ÓŠ2ĆūʶĄ§ÉśµÄ°ą¼¶ÓŠ20©5©6©5©2=2£Øøö£©£¬
²¹Č«ĢõŠĪĶ¼ČēĶ¼£ŗ
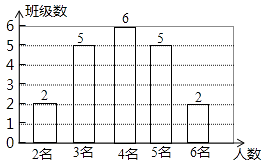
£Ø2£©½ā£ŗøł¾ŻĢāŅā£¬½«Į½øö°ą¼¶4Ćūѧɜ·Ö±š¼Ē×÷A1”¢A2”¢B1”¢B2£¬
ĮŠ±ķČēĻĀ£ŗ
A1 | A2 | B1 | B2 | |
A1 | A1£¬A2 | A1£¬B1 | A1£¬B2 | |
A2 | A2£¬A1 | A2£¬B1 | A2£¬B2 | |
B1 | B1£¬A1 | B1£¬A2 | B1£¬B2 | |
B2 | B2£¬A1 | B2£¬A2 | B2£¬B1 |
ÓÉÉĻ±ķæÉÖŖ£¬“ÓÕāĮ½øö°ą¼¶ČĪŃ”Į½Ćūѧɜ½ųŠŠ°ļ·ö¹²ÓŠ12ÖÖµČæÉÄܽį¹ū£¬ĘäÖŠ±»Ń”ÖŠµÄĮ½ĆūѧɜĄ“×ŌĶ¬Ņ»°ą¼¶µÄÓŠ4ÖÖ½į¹ū£¬
”ą±»Ń”ÖŠµÄĮ½ĆūѧɜĄ“×ŌĶ¬Ņ»°ą¼¶µÄøÅĀŹĪŖ ![]() =
= ![]()
”¾½āĪö”æ£Ø1£©øł¾ŻĮōŹŲ¶łĶÆÓŠ4ĆūµÄ°ą¼¶ÓŠ6øö£¬Õ¼30%£¬æÉĒóµĆÓŠĮōŹŲ¶łĶƵİą¼¶×ÜŹż£¬ŌŁĒóµĆĮōŹŲ¶łĶÆŹĒ2ĆūµÄ°ąŹż£»£Ø2£©ÓÉ£Ø1£©µĆÖ»ÓŠ2ĆūĮōŹŲ¶łĶƵİą¼¶ÓŠ2øö£¬¹²4Ćūѧɜ£®ÉčA1£¬A2Ą“×ŌŅ»øö°ą£¬B1£¬B2Ą“×ŌŅ»øö°ą£¬ĮŠ±ķæÉµĆ³öĄ“×ŌŅ»øö°ąµÄ¹²ÓŠ4ÖÖĒéæö£¬¼Ģ¶ųæɵĆĖłŃ”Į½ĆūĮōŹŲ¶łĶÆĄ“×ŌĶ¬Ņ»øö°ą¼¶µÄøÅĀŹ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖµćDŌŚ·“±ČĄżŗÆŹży= ![]() µÄĶ¼ĻóÉĻ£¬¹żµćD×÷xÖįµÄĘ½ŠŠĻß½»yÖįÓŚµćB£Ø0£¬3£©£®¹żµćA£Ø5£¬0£©µÄÖ±Ļßy=kx+bÓėyÖįÓŚµćC£¬ĒŅBD=OC£¬tan”ĻOAC=
µÄĶ¼ĻóÉĻ£¬¹żµćD×÷xÖįµÄĘ½ŠŠĻß½»yÖįÓŚµćB£Ø0£¬3£©£®¹żµćA£Ø5£¬0£©µÄÖ±Ļßy=kx+bÓėyÖįÓŚµćC£¬ĒŅBD=OC£¬tan”ĻOAC= ![]() £®
£®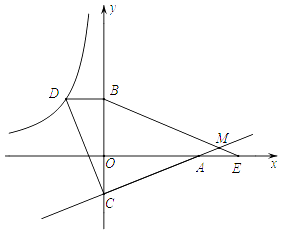
£Ø1£©Ē󷓱ȥżŗÆŹży= ![]() ŗĶÖ±Ļßy=kx+bµÄ½āĪöŹ½£»
ŗĶÖ±Ļßy=kx+bµÄ½āĪöŹ½£»
£Ø2£©Į¬½ÓCD£¬ŹŌÅŠ¶ĻĻ߶ĪACÓėĻ߶ĪCDµÄ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø3£©µćEĪŖxÖįÉĻµćAÓŅ²ąµÄŅ»µć£¬ĒŅAE=OC£¬Į¬½ÓBE½»Ö±ĻßCAÓėµćM£¬Ēó”ĻBMCµÄ¶ČŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬AB”ĪEF£¬BC”ĶCDÓŚµćC£¬”ĻABC£½30”ć£¬”ĻDEF£½45”ć£¬Ōņ”ĻCDEµČÓŚ(””””)

A. 105”ć B. 75”ć C. 135”ć D. 115”ć
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚŹżÖįÉĻµć A ±ķŹ¾µÄÓŠĄķŹżĪŖ©4£¬µć B ±ķŹ¾µÄÓŠĄķŹżĪŖ 6£¬µć P “Ó µć A ³ö·¢ŅŌĆæĆė 2 øöµ„Ī»³¤¶ČµÄĖŁ¶ČŌŚŹżÖįÉĻŃŲÓÉ A µ½ B ·½ĻņŌĖ¶Æ£¬µ±µć P µ½ “ļµć B ŗóĮ¢¼“·µ»Ų£¬ČŌČ»ŅŌĆæĆė 2 øöµ„Ī»³¤¶ČµÄĖŁ¶ČŌĖ¶ÆÖĮµć A Ķ£Ö¹ŌĖ¶Æ£®Éč ŌĖ¶ÆŹ±¼äĪŖ t£Øµ„Ī»£ŗĆė£©£®
£Ø1£©Ēó t=2 Ź±µć P ±ķŹ¾µÄÓŠĄķŹż£»
£Ø2£©Ēóµć P ŹĒ AB µÄÖŠµćŹ± t µÄÖµ£»
£Ø3£©ŌŚµć P Óɵć A µ½µć B µÄŌĖ¶Æ¹ż³ĢÖŠ£¬Ēóµć P Óėµć A µÄ¾ąĄė£ØÓĆŗ¬ t µÄ“śŹżŹ½±ķŹ¾£©£»
£Ø4£©ŌŚµć P Óɵć B µ½µć A µÄ·µ»Ų¹ż³ĢÖŠ£¬µć P ±ķŹ¾µÄÓŠĄķŹżŹĒ¶ąÉŁ£ØÓĆŗ¬ t µÄ “śŹżŹ½±ķŹ¾£©£®
![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŌĮāŠĪABCD¶Ō½ĒĻß½»µćĪŖ×ų±źŌµć£¬½ØĮ¢Ę½ĆęÖ±½Ē×ų±źĻµ£¬A”¢BĮ½µćµÄ×ų±ź·Ö±šĪŖ£Ø©2 ![]() £¬0£©”¢£Ø0£¬©
£¬0£©”¢£Ø0£¬© ![]() £©£¬Ö±ĻßDE”ĶDC½»ACÓŚE£¬¶ÆµćP“ÓµćA³ö·¢£¬ŅŌĆæĆė2øöµ„Ī»µÄĖŁ¶ČŃŲ×ÅA”śD”śCµÄĀ·ĻßĻņÖÕµćCŌČĖŁŌĖ¶Æ£¬Éč”÷PDEµÄĆ껿ĪŖS£ØS”Ł0£©£¬µćPµÄŌĖ¶ÆŹ±¼äĪŖtĆė£®
£©£¬Ö±ĻßDE”ĶDC½»ACÓŚE£¬¶ÆµćP“ÓµćA³ö·¢£¬ŅŌĆæĆė2øöµ„Ī»µÄĖŁ¶ČŃŲ×ÅA”śD”śCµÄĀ·ĻßĻņÖÕµćCŌČĖŁŌĖ¶Æ£¬Éč”÷PDEµÄĆ껿ĪŖS£ØS”Ł0£©£¬µćPµÄŌĖ¶ÆŹ±¼äĪŖtĆė£®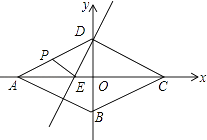
£Ø1£©ĒóÖ±ĻßDEµÄ½āĪöŹ½£»
£Ø2£©ĒóSÓėtÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³ö×Ō±äĮætµÄȔֵ·¶Ī§£»
£Ø3£©µ±tĪŖŗĪÖµŹ±£¬”ĻEPD+”ĻDCB=90”ć£æ²¢Ēó³ö“ĖŹ±Ö±ĻßBPÓėÖ±ĻßACĖł¼ŠČń½ĒµÄÕżĒŠÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ“Ó2017ğʚ£¬Ą„Ć÷½«ÓĄ“”°øßĢśŹ±“ś”±£¬Õā¾ĶŅāĪ¶×ŽńŗóĄ„Ć÷µÄŹŠĆńĶā³öĀĆŠŠµÄĀ·³ĢÓėŹ±¼ä½«“ó“óĖõ¶Ģ£¬µ«Ņ²ÓŠ²»ÉŁÓĪæĶøł¾Ż×Ō¼ŗµÄĻ²ŗĆŅĄČ»Ń”Ōń³Ė×ųĘÕĶØĮŠ³µ£»ŅŃÖŖ“ÓĄ„Ć÷µ½Ä³ŹŠµÄøßĢśŠŠŹ»Ā·³ĢŹĒ400Ē§Ć×£¬ĘÕĶØĮŠ³µµÄŠŠŹ»Ā·³ĢŹĒøßĢśŠŠŹ»Ā·³ĢµÄ1.3±¶£¬ĒėĶź³ÉŅŌĻĀĪŹĢā£ŗ(1)ĘÕĶØĮŠ³µµÄŠŠŹ»Ā·³ĢĪŖ________Ē§Ć×£»(2)ČōøßĢśµÄĘ½¾łĖŁ¶Č£ØĒ§Ć×/Ź±£©ŹĒĘÕĶØĮŠ³µĘ½¾łĖŁ¶Č£ØĒ§Ć×/Ź±£©µÄ2.5±¶£¬ĒŅ³Ė×ųøßĢśĖłŠčŹ±¼ä±Č³Ė×ųĘÕĶØĮŠ³µĖłŠčŹ±¼äĖõ¶Ģ3Š”Ź±£¬ĒóĘÕĶØĮŠ³µŗĶøßĢśµÄĘ½¾łĖŁ¶Č£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ ”÷ABC ÖŠ£¬”ĻC=90”ć£¬DB”ĶBC ÓŚµć £¬·Ö±šŅŌµć D ŗĶµć ĪŖŌ²ŠÄ£¬ŅŌ“óÓŚ![]() µÄ³¤ĪŖ°ė¾¶×÷»”£¬Į½»”Ļą½»ÓŚµć E ŗĶµć £¬×÷Ö±Ļß EF£¬ŃÓ³¤ AB ÓŚµć £¬Į¬½Ó DG£¬ĻĀĆęŹĒĖµĆ÷ ”ĻA=”ĻD µÄĖµĄķ¹ż³Ģ£¬Ēė°ŃĻĀĆęµÄĖµĄķ¹ż³Ģ²¹³äĶźÕū£ŗ
µÄ³¤ĪŖ°ė¾¶×÷»”£¬Į½»”Ļą½»ÓŚµć E ŗĶµć £¬×÷Ö±Ļß EF£¬ŃÓ³¤ AB ÓŚµć £¬Į¬½Ó DG£¬ĻĀĆęŹĒĖµĆ÷ ”ĻA=”ĻD µÄĖµĄķ¹ż³Ģ£¬Ēė°ŃĻĀĆęµÄĖµĄķ¹ż³Ģ²¹³äĶźÕū£ŗ
ŅņĪŖ DB”ĶBC£ØŅŃÖŖ£©£¬
ĖłŅŌ ”ĻDBC=90”ć( ) £®
ŅņĪŖ ”ĻC=90”ć£ØŅŃÖŖ£©£¬
ĖłŅŌ ”ĻDBC=”ĻC£ØµČĮæ“ś»»£©£¬
ĖłŅŌ DB”ĪAC ( ) £¬
ĖłŅŌ £ØĮ½Ö±ĻßĘ½ŠŠ£¬Ķ¬Ī»½ĒĻąµČ£©£»
ÓÉ×÷Ķ¼·ØæÉÖŖ£ŗÖ±Ļß EF ŹĒĻ߶Ī DB µÄ ( ) £¬
ĖłŅŌ GD=GB£¬Ļ߶Ī £ØÉĻµÄµćµ½Ļ߶ĪĮ½¶ĖµćµÄ¾ąĄėĻąµČ£©£¬
ĖłŅŌ ( ) £¬ŅņĪŖ ”ĻA=”Ļ1£ØŅŃÖŖ£©£¬
ĖłŅŌ ”ĻA=”ĻD£ØµČĮæ“ś»»£©£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µćEŹĒÕż·½ŠĪABCD¶Ō½ĒĻßACÉĻŅ»µć£¬EF”ĶAB£¬EG”ĶBC£¬“¹×ć·Ö±šĪŖF£¬G£¬ČōÕż·½ŠĪABCDµÄÖܳ¤ŹĒ40cm.
(1)ĒóÖ¤£ŗĖıߊĪBFEGŹĒ¾ŲŠĪ£»
(2)ĒóĖıߊĪEFBGµÄÖܳ¤£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij°ąŹżŃ§æĪĶā»ī¶ÆŠ”×éµÄĶ¬Ń§Óū²āĮ湫Ō°ÄŚŅ»æĆŹ÷DEµÄøß¶Č£¬ĖūĆĒŌŚÕāæĆŹ÷ÕżĒ°·½Ņ»Ā„Ķ¤Ē°µÄĢؽ×ÉĻAµć“¦²āµĆŹ÷¶„¶ĖDµÄŃö½ĒĪŖ30”ć£¬³Æ×ÅÕāæĆŹ÷µÄ·½Ļņ×ßµ½Ģؽ×ĻĀµÄµćC“¦²āµĆŹ÷¶„¶ĖDµÄŃö½ĒĪŖ60”ć£¬ŅŃÖŖAµćµÄø߶ČABĪŖ2Ć×£¬Ģؽ×ACµÄĘĀ¶Či=1£ŗ2£¬ĒŅB£¬C£¬EČżµćŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬Ēėøł¾ŻŅŌÉĻĢõ¼žĒó³öŹ÷DEµÄøß¶Č£®£Ø²āĒćĘ÷µÄø߶ČŗöĀŌ²»¼Ę£¬½į¹ū±£ĮōøłŗÅ£© 
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com