
如图(1),分别以两个彼此相邻的正方形OABC与CDEF的边OC、OA所在直线为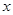 轴、
轴、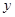 轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在
轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在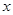 轴上)交y轴于另一点Q,抛物线
轴上)交y轴于另一点Q,抛物线 经过A、C两点,与
经过A、C两点,与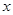 轴的另一交点为G,M是FG的中点,B点坐标为(2,2).
轴的另一交点为G,M是FG的中点,B点坐标为(2,2).
【小题1】求抛物线的函数解析式和点E的坐标;
【小题2】求证:ME是⊙P的切线;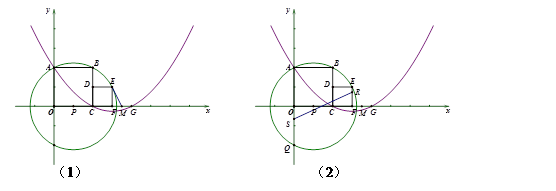
【小题1】解:如图甲,连接PE、PB,设PC=n,
∵正方形CDEF的面积为1,
∴CD=CF=1,
根据圆和正方形的对称性知:OP=PC=n,
∴BC=2PC=2n,
∵而PB=PE,
∴PB2=BC2+PC2=4n2+n2=5n2,PE2=PF2+EF2=(n+1)2+1,
∴5n2=(n+1)2+1,
解得:n=1或n=- (舍去),
(舍去),
∴BC=OC=2,
∴B点坐标为(2,2);(6分)
【小题2】证明:如图甲,由(1)知A(0,2),C(2,0),
∵A,C在抛物线上,
∴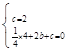 ,
,
解得: ,
,
∴抛物线的解析式为:y= x2-
x2-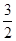 x+2=
x+2= (x-3)2-
(x-3)2- ,
,
∴抛物线的对称轴为x=3,即EF所在直线,
∵C与G关于直线x=3对称,
∴CF=FG=1,
∴MF= FG=
FG= ,
,
在Rt△PEF与Rt△EMF中,
∠EFM=∠EFP,
∵ ,
, ,
,
∴ ,
,
∴△PEF∽△EMF,
∴∠EPF=∠FEM,
∴∠PEM=∠PEF+∠FEM=∠PEF+∠EPF=90°,
∴ME是⊙P的切线;(12分)
解析


 53天天练系列答案
53天天练系列答案科目:初中数学 来源:2012-2013学年江西省吉安市朝宗实验学校九年级(下)第一次段考数学试卷(解析版) 题型:填空题
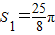 ,S2=2π,则S3是 .
,S2=2π,则S3是 .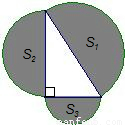
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com