
| x+1 |
| x-1 |
| x-1 |
| x+1 |
| 2x+a+2 |
| x2-1 |
| 7 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| 7 |
| 2 |
| 7 |
| 2 |
| 31 |
| 2 |
| 31 |
| 2 |


科目:初中数学 来源: 题型:阅读理解
| a |
| b |
| ab |
| ab |
| ab |
| p |
| p |
| 1 |
| m |
| ab |
| 12 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| ||
| k |
查看答案和解析>>
科目:初中数学 来源: 题型:
| ||
| k |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
| ||
| k |
查看答案和解析>>
科目:初中数学 来源:第1章《反比例函数》常考题集(17):1.3 实际生活中的反比例函数(解析版) 题型:解答题
 ≥0,∴a-
≥0,∴a-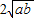 +b≥0,∴a+b≥2
+b≥0,∴a+b≥2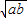 ,只有点a=b时,等号成立.
,只有点a=b时,等号成立.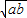 (a,b均为正实数)中,若ab为定值p,则a+b≥
(a,b均为正实数)中,若ab为定值p,则a+b≥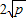 ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2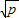 .
.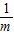 有最小值______;
有最小值______;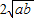 ,并指出等号成立时的条件;
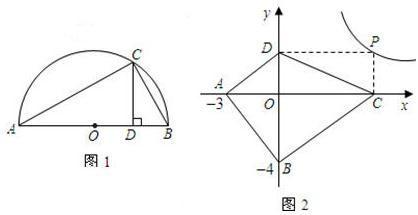
,并指出等号成立时的条件; 上的任意一点,过点P作PC⊥x轴于点C,PO⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
上的任意一点,过点P作PC⊥x轴于点C,PO⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.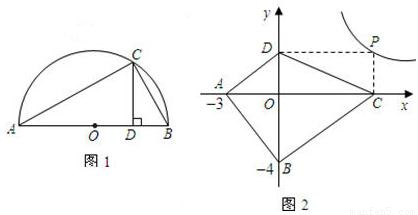
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com