
分析 本题考虑两种情形:①如图1中,当∠BAD是钝角时,设AB=a,BC=b,列方程组求出a、b,再利用勾股定理求出BE、DF,即可解决问题.②如图2中,当∠BAD是锐角时,求出CE、CF即可.
解答 解:①如图1中,当∠BAD是钝角时,设AB=a,BC=b,
∵四边形ABCD是平行四边形,
∴AB=CD=a,$\frac{1}{2}$•BC•AE=$\frac{1}{2}$•CD•AF, ∴3a=2b ①
∴3a=2b ①
∵a+b=20 ②
由①②解得a=8,b=12,
在RT△ABE中,∵∠AEB=90°,AB=8,AE=4,
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∴EC=12-4$\sqrt{3}$,
在RT△ADF中,∵∠AFD=90°.AD=12,AF=6.
∴DF=$\sqrt{A{D}^{2}-A{F}^{2}}$=6$\sqrt{3}$,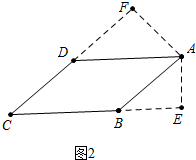
∵6$\sqrt{3}$>8,
∴CF=DF-CD=6$\sqrt{3}$-8,
∴CE+CF=EC+CF=4+2$\sqrt{3}$.
②如图2中,当∠BAD是锐角时,由①可知:DF=6$\sqrt{3}$,BE=4$\sqrt{3}$,
∴CF=8+6$\sqrt{3}$,CE=12+4$\sqrt{3}$,
∴CE+CF=20+10$\sqrt{3}$.
故答案为$20+10\sqrt{3}$或$4+2\sqrt{3}$
点评 本题考查平行四边形的性质、勾股定理等知识,解题的关键是正确画出图形,注意本题有两个解,通过计算确定高的位置,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
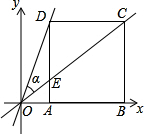 边长为2的正方形ABCD在平面直角坐标系中如图放置,已知点A的横坐标为1,作直线OC与边AD交于点E.
边长为2的正方形ABCD在平面直角坐标系中如图放置,已知点A的横坐标为1,作直线OC与边AD交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
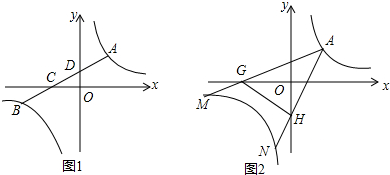
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
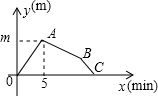 哥哥和弟弟同时从家沿同一条路去同一所学校上学,弟弟步行,哥哥骑自行车,两人都匀速前进.弟弟步行每分钟走60米,哥哥骑自行车每分钟行驶160米.如图是两人之间的距离y与弟弟步行时间x之间的函数图象.请解答下列问题.
哥哥和弟弟同时从家沿同一条路去同一所学校上学,弟弟步行,哥哥骑自行车,两人都匀速前进.弟弟步行每分钟走60米,哥哥骑自行车每分钟行驶160米.如图是两人之间的距离y与弟弟步行时间x之间的函数图象.请解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
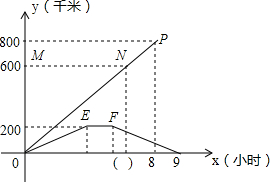 在笔直的公路上依次有A,B,C三地,甲车从A地出发速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地停留1小时后,按原速返回到C地,在两车行驶的过程中,甲、乙两车距各自出发的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象回答下列问题:
在笔直的公路上依次有A,B,C三地,甲车从A地出发速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地停留1小时后,按原速返回到C地,在两车行驶的过程中,甲、乙两车距各自出发的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com