
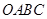 是一张放在平面直角坐标系中的矩形纸片,
是一张放在平面直角坐标系中的矩形纸片,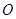 为原点,点
为原点,点 在
在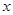 轴的正半轴上,
轴的正半轴上,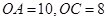 ,在
,在 上取一点
上取一点 ,将纸片沿
,将纸片沿 翻折,使点
翻折,使点 落在
落在 边上的点
边上的点 处,求直线
处,求直线 的解析式.
的解析式.
 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源:不详 题型:解答题
 (x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。
(x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
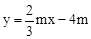 与x轴、y轴分别交于点A、B,点C在线段AB上,且
与x轴、y轴分别交于点A、B,点C在线段AB上,且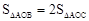 .
.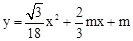 上时,求该抛物线的表达式;
上时,求该抛物线的表达式;
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
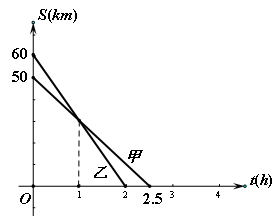
 两地去同一城市,它们离
两地去同一城市,它们离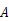 地的路程随时间变化的图像如图所示,则下列结论错误的是( )
地的路程随时间变化的图像如图所示,则下列结论错误的是( ) 
A.摩托车比汽车晚到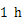 |
B. 两地的路程为 两地的路程为 |
C.摩托车的速度为 |
D.汽车的速度为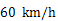 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
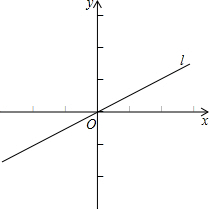
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com