
【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.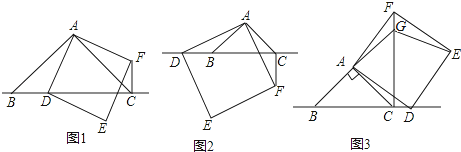
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为:;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2 ![]() ,CD=
,CD= ![]() BC,请求出GE的长.
BC,请求出GE的长.
【答案】
(1)垂直;BC=CF+CD
(2)
证明:成立,
∵正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中,  ,
,
∴△DAB≌△FAC,
∴∠B=∠ACF,CF=BD
∴∠ACB+∠ACF=90°,即CF⊥BD;
∵BC=BD+CD,
∴BC=CF+CD
(3)
解: 过A作AH⊥BC于H,过E作EM⊥BD于M,EN⊥CF于N,

∵∠BAC=90°,AB=AC,
∴BC= ![]() AB=4,AH=
AB=4,AH= ![]() BC=2,
BC=2,
∴CD= ![]() BC=1,CH=
BC=1,CH= ![]() BC=2,
BC=2,
∴DH=3,
由(2)证得BC⊥CF,CF=BD=5,
∵四边形ADEF是正方形,
∴AD=DE,∠ADE=90°,
∵BC⊥CF,EM⊥BD,EN⊥CF,
∴四边形CMEN是矩形,
∴NE=CM,EM=CN,
∵∠AHD=∠ADC=∠EMD=90°,
∴∠ADH+∠EDM=∠EDM+∠DEM=90°,
∴∠ADH=∠DEM,
在△ADH与△DEM中,  ,
,
∴△ADH≌△DEM,
∴EM=DH=3,DM=AH=2,
∴CN=EM=3,EN=CM=3,
∵∠ABC=45°,
∴∠BGC=45°,
∴△BCG是等腰直角三角形,
∴CG=BC=4,
∴GN=1,
∴EG= ![]() =
= ![]() .
.
【解析】解:(1)①正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中,  ,
,
∴△DAB≌△FAC,
∴∠B=∠ACF,
∴∠ACB+∠ACF=90°,即CF⊥BD;
故答案为:垂直;
②△DAB≌△FAC,
∴CF=BD,
∵BC=BD+CD,
∴BC=CF+CD;
故答案为:BC=CF+CD;
(1)①根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB≌△FAC,根据全等三角形的性质即可得到结论;②由正方形ADEF的性质可推出△DAB≌△FAC,根据全等三角形的性质得到CF=BD,∠ACF=∠ABD,根据余角的性质即可得到结论;(2)根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB≌△FAC,根据全等三角形的性质即可得到结论(3)根据等腰直角三角形的性质得到BC= ![]() AB=4,AH=
AB=4,AH= ![]() BC=2,求得DH=3,根据正方形的性质得到AD=DE,∠ADE=90°,根据矩形的性质得到NE=CM,EM=CN,由角的性质得到∠ADH=∠DEM,根据全等三角形的性质得到EM=DH=3,DM=AH=2,等量代换得到CN=EM=3,EN=CM=3,根据等腰直角三角形的性质得到CG=BC=4,根据勾股定理即可得到结论.本题考查了全等三角形的判定和性质,正方形的性质,余角的性质,勾股定理,等腰直角三角形的判定和性质,矩形的判定和性质,正确的作出辅助线构造全等三角形是解题的关键.
BC=2,求得DH=3,根据正方形的性质得到AD=DE,∠ADE=90°,根据矩形的性质得到NE=CM,EM=CN,由角的性质得到∠ADH=∠DEM,根据全等三角形的性质得到EM=DH=3,DM=AH=2,等量代换得到CN=EM=3,EN=CM=3,根据等腰直角三角形的性质得到CG=BC=4,根据勾股定理即可得到结论.本题考查了全等三角形的判定和性质,正方形的性质,余角的性质,勾股定理,等腰直角三角形的判定和性质,矩形的判定和性质,正确的作出辅助线构造全等三角形是解题的关键.


科目:初中数学 来源: 题型:
【题目】(1)问题如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°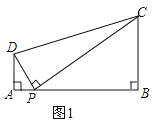
(1)求证:ADBC=APBP
(2)探究如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)应用请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A,设点P的运动时间为t(秒),当以D为圆心,以DC为半径的圆与AB相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.
(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?(不需说明理由)
②是否存在满足条件的点P,使得PC= ![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市南县大力发展农村旅游事业,全力打造“洞庭之心湿地公园”,其中罗文村的“花海、涂鸦、美食”特色游享誉三湘,游人如织.去年村民罗南洲抓住机遇,返乡创业,投入20万元创办农家乐(餐饮+住宿),一年时间就收回投资的80%,其中餐饮利润是住宿利润的2倍还多1万元.
(1)求去年该农家乐餐饮和住宿的利润各为多少万元?
(2)今年罗南洲把去年的餐饮利润全部用于继续投资,增设了土特产的实体店销售和网上销售项目.他在接受记者采访时说:“我预计今年餐饮和住宿的利润比去年会有10%的增长,加上土特产销售的利润,到年底除收回所有投资外,还将获得不少于10万元的纯利润.”请问今年土特产销售至少有多少万元的利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,△ABC中,∠ABC、∠ACB的平分线交于O点,过O点作EF∥BC交AB、AC于点E、F.试猜想EF、BE、CF之间有怎样的关系,并说明理由.


(2)如图,若将图①中∠ACB的平分线改为外角∠ACD的平分线,其它条件不变,则刚才的结论还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=3,BC=5,点E、F是BC、CD边上的动点(包括端点处),若将纸片沿EF折叠,使得点C恰好落在AD边上点P处.设CF=x,则x的取值范围为 . 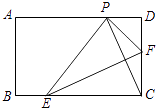
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com