
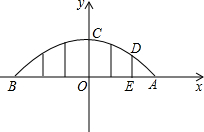
 抛物线关于y轴对称,顶点C坐标为(0,9),交x轴于点A(d,0),B(-d,0)(d>0),如图将ABC视为抛物线形拱桥,五根拉杆均垂直于x轴,垂足依次在线段AB的6等分点上,h=9m,求拉杆DE的长度.
抛物线关于y轴对称,顶点C坐标为(0,9),交x轴于点A(d,0),B(-d,0)(d>0),如图将ABC视为抛物线形拱桥,五根拉杆均垂直于x轴,垂足依次在线段AB的6等分点上,h=9m,求拉杆DE的长度. 分析 根据顶点坐标设抛物线解析式为y=ax2+9,将点A坐标代入求得a,即可表示出抛物线解析式,再将x=$\frac{2}{3}$d代入即可求得DE的长.
解答 解:设抛物线解析式为y=ax2+9,
将点A(d,0)代入,得:ad2+9=0,
解得:a=-$\frac{9}{{d}^{2}}$,
∴抛物线解析式为:y=-$\frac{9}{{d}^{2}}$x2+9,
根据题意,当x=$\frac{2}{3}$d时,y=-$\frac{9}{{d}^{2}}$×($\frac{2}{3}$d)2+9=5,
答:拉杆DE的长度为5m.
点评 本题主要考查二次函数的实际应用,根据题意用含d的式子表示出抛物线解析式是解题的关键.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题
 已知:如图,AD=CD=CB=AB=a,DA∥CB,AB⊥CB,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.
已知:如图,AD=CD=CB=AB=a,DA∥CB,AB⊥CB,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC是等边三角形,P是∠ABC平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q,若BQ=2,则PE的长是2.
如图,△ABC是等边三角形,P是∠ABC平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q,若BQ=2,则PE的长是2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在一山顶有铁搭AB,从点P到铁塔底部B点有一条索道PB,该索道长为200米,在P处测得B点的仰角为a=30°,在P处测得A点的仰角为β=45°,则铁塔的高AB为(100$\sqrt{3}$-100)米.
在一山顶有铁搭AB,从点P到铁塔底部B点有一条索道PB,该索道长为200米,在P处测得B点的仰角为a=30°,在P处测得A点的仰角为β=45°,则铁塔的高AB为(100$\sqrt{3}$-100)米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com