解:(1)Rt△ACB中,OC⊥AB,AO=1,BO=4;
由射影定理,得:OC
2=OA•OB=4,则OC=2,即点C(0,2);
设抛物线的解析式为:y=a(x+1)(x-4),将C点代入上式,得:
2=a(0+1)(0-4),a=-

,
∴抛物线的解析式:y=-

(x+1)(x-4)=-

x
2+

x+2;
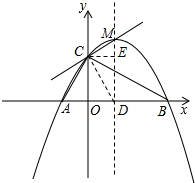
(2)直线CM与以AB为直径的圆相切.理由如下:
如右图,设抛物线的对称轴与x轴的交点为D,连接CD.
由于A、B关于抛物线的对称轴对称,则点D为Rt△ABC斜边AB的中点,CD=

AB.
由(1)知:y=-

(x+1)(x-4)=-

(x-

)
2+
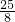
,
则点M(

,
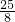
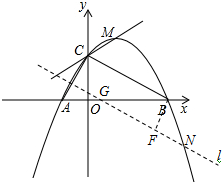
),ME=
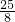
-2=
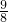
;
而CE=OD=

,OC=2;
∴ME:CE=OD:OC,又∠MEC=∠COD=90°,
∴△COD∽△CEM,
∴∠CME=∠CDO,
∴∠CME+∠CDM=∠CDO+∠CDM=90°,
而CD等于⊙D的半径长,所以直线CM与以AB为直径的圆相切;
(3)由B(4,0)、C(0,2)得:BC=2

;
则:S
△BCN=

BC•h=

×2

×h=4,h=
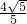
;
过点B作BF⊥BC,且使BF=h=
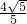
,过F作直线l∥BC交x轴于G.
Rt△BFG中,sin∠BGF=sin∠CBO=
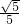
,BG=BF÷sin∠BGF=
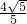
÷
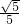
=4;
∴G(0,0)或(8,0).
易知直线BC:y=-

x+2,则可设直线l:y=-

x+b,代入G点坐标,得:b=0或b=4,则:
直线l:y=-

x或y=-

x+4;
联立抛物线的解析式后,可得:
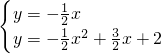
或

,
则 N
1(2+2

,-1-

)、N
2(2-2

,-1+

)、N
3(2,3).
分析:(1)Rt△ACB中,OC⊥AB,利用射影定理能求出OC的长,即可确定C点坐标,再利用待定系数法能求出该抛物线的解析式.
(2)此题的解法有两种:①过AB的中点作直线CM的垂线,比较该垂线段与AB的一半(半径)的大小关系,若两者相等,则直线CM与AB为直径的圆相切;若该垂线段小于半径长,则两者的位置关系为相交;若该垂线段大于半径长,则两者的位置关系为相离;
②连接AB中点(设为点D)和点C,根据直角三角形的性质知:CD为⊙D的半径长,那么只需判断CD是否与CM垂直即可,若垂直,则直线CM与⊙D相切;若不垂直,则相交.
(3)先求出线段BC的长,根据△BCN的面积,可求出BC边上的高,那么做直线l,且直线l与直线BC的长度正好等于BC边上的高,那么直线l与抛物线的交点即为符合条件的N点.
点评:该题考查了二次函数解析式的确定、函数图象交点坐标的求法、图形面积的求法以及直线与圆的位置关系等重点知识,(3)题中,直线l可能在B点左侧也可能在其右侧,一定要将所有情况都考虑到.

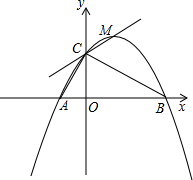 y=ax2+bx+c经过A、B、C三点,其顶点为M.
y=ax2+bx+c经过A、B、C三点,其顶点为M. ,
, (x+1)(x-4)=-
(x+1)(x-4)=- x2+
x2+ x+2;
x+2; (2)直线CM与以AB为直径的圆相切.理由如下:
(2)直线CM与以AB为直径的圆相切.理由如下: AB.
AB. (x+1)(x-4)=-
(x+1)(x-4)=- (x-
(x- )2+
)2+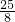 ,
, ,
,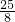 ),ME=
),ME=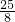 -2=
-2=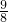 ;
; ,OC=2;
,OC=2; (3)由B(4,0)、C(0,2)得:BC=2
(3)由B(4,0)、C(0,2)得:BC=2 ;
; BC•h=
BC•h= ×2
×2 ×h=4,h=
×h=4,h=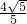 ;
;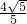 ,过F作直线l∥BC交x轴于G.
,过F作直线l∥BC交x轴于G.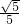 ,BG=BF÷sin∠BGF=
,BG=BF÷sin∠BGF=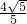 ÷
÷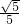 =4;
=4; x+2,则可设直线l:y=-
x+2,则可设直线l:y=- x+b,代入G点坐标,得:b=0或b=4,则:
x+b,代入G点坐标,得:b=0或b=4,则: x或y=-
x或y=- x+4;
x+4;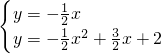 或
或 ,
, ,-1-
,-1- )、N2(2-2
)、N2(2-2 ,-1+
,-1+ )、N3(2,3).
)、N3(2,3).

 阅读快车系列答案
阅读快车系列答案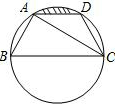 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )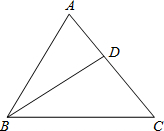 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设