练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列图形中，既是中心对称图形又是轴对称图形的是（　　）

    A. B. C. D.

    D 【解析】根据中心对称图形和轴对称图形的定义即可判断. 【解析】 A、是中心对称图形，不是轴对称图形，故本选项错误； B、不是中心对称图形，是轴对称图形，故本选项错误； C、不是中心对称图形，是轴对称图形，故本选项错误； D、既是中心对称图形又是轴对称图形，故本选项正确． 故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：安徽省蚌埠市2017届九年级下学期中考二模数学试卷 题型：解答题

    近年来，某市旅游事业蓬勃发展，吸引大批海内外游客前来观光旅游、购物度假，下面两图分别反映了该市2013——2016年游客总人数和旅游业总收入情况.

    根据统计图提供的信息，解答下列问题：

    （1）2016年游客总人数为 万人次，旅游业总收入为 万元；

    （2）在2014年，2015年，2016年这三年中，旅游业总收入增长幅度最大的是 年，这一年的旅游业总收入比上一年增长的百分率为 （精确到0.1%）；

    （3）2016年的游客中，国内游客为1200万人次，其余为海外游客，据统计，国内游客的人均消费约为700元，问海外游客的人均消费约为多少元？（注：旅游收入=游客人数×游客的人均消费）

    (1) 1225,940000；(2) 2004,41.4%；(3) 海外游客的人均消费约为4000元. 【解析】试题分析：由统计图可知： （1）2016年游客总人数为1225万人次，旅游业总收入为940000万元； （2）在2014年，2015年，2016年这三年中，旅游业总收入增长幅度最大的是2014年，这一年比上一年增长的百分率为（940000-665000）÷665000...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十七章 达标检测卷 题型：单选题

    如图，在△ABC中，点D，E，F分别在边AB，AC，BC上，若DE∥BC，EF∥AB，则下面所列比例式中正确的是（　　）

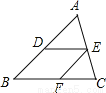
    A. B. C. D.

    C 【解析】试题解析：∵DE∥BC， BD≠BC， ∴，选项A不正确； ∴，选项B不正确； ∴，选项C正确； 选项D不正确； 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年甘肃省武威市凉州区洪祥镇九年级（上）期末数学试卷 题型：填空题

    方程x2﹣9x+18=0的两个根是等腰三角形的底和腰的长，则这个等腰三角形的周长为_____．

    15 【解析】试题解析：x2-9x+18=0， （x-3）（x-6）=0， 所以x1=3，x2=6， 所以等腰三角形的底为3，腰为6，这个等腰三角形的周长为3+6+6=15．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年甘肃省武威市凉州区洪祥镇九年级（上）期末数学试卷 题型：单选题

    如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD＝55°，则∠BCD的度数为(　　)

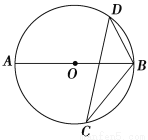
    A．35° B．45°

    C．55° D．75°

    A 【解析】连接AD， ∵AB是⊙O的直径， ∴∠ADB＝90°， ∵∠ABD＝55°， ∴∠A＝90°－∠ABD＝35°， ∴∠BCD＝∠A＝35°.

    查看答案和解析>>

    科目：初中数学 来源：浙江杭州建德2016-2017学年七年级上学期期末数学试卷 题型：解答题

    先化简再求值，已知，求代数式的值．

    －12 【解析】试题分析：根据非负数的性质，求出a、b、c的值，化简整式然后把a、b、c的值代入计算即可． 试题解析：【解析】 ∵， ， ， ， ∴， ， ， ∴， ． 原式． 当a=6，b=2，c=－1时，原式=6×2×（－1）=－12．

    查看答案和解析>>

    科目：初中数学 来源：浙江杭州建德2016-2017学年七年级上学期期末数学试卷 题型：填空题

    若是关于的方程的解，则的值为_________．

    【解析】【解析】 ∵x=2是方程2x-m+6=0的解，∴2×2-m+6=0，解得：m=10．故答案为：10．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级下册 期中测试卷 题型：解答题

    如图，已知梯形ABCD，AB∥DC，△AOB的面积等于9，△AOD的面积等于6，AB＝7，求CD的长．

    【解析】试题分析： 由题意易得△COD∽△AOB，由此可得： ；由△AOB的面积等于9，△AOD的面积等于6，可得： ，再结合AB=7即可求得CD的长. 试题解析： ∵AB∥DC， ∴△COD∽△AOB， ∴， ∵△AOB的面积等于9，△AOD的面积等于6， ∴， ∴， 又∵AB＝7， ∴， ∴CD＝.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学人教版上册：第4章 几何图形初步 单元测试卷 题型：解答题

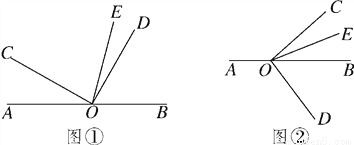
    （12分）已知O是直线AB上的一点，∠COD是直角，OE平分∠BOC.

    （1）如图①，若∠AOC＝30°，求∠DOE的度数；

    （2）在图①中，若∠AOC＝a，直接写出∠DOE的度数（用含a的代数式表示）；

    （3）将图①中的∠DOC绕顶点O顺时针旋转至图②的位置.

    ①探究∠AOC和∠DOE的度数之间的关系，写出你的结论，并说明理由；

    ②在∠AOC的内部有一条射线OF，且∠AOC－4∠AOF＝2∠BOE＋∠AOF，试确定∠AOF与∠DOE的度数之间的关系，说明理由.

    （1）15°；（2）；（3）①∠AOC＝2∠DOE；②4∠DOE－5∠AOF＝180°. 【解析】试题分析：(1)由已知可求出∠BOC=180°-∠AOC=150°，再由∠COD是直角，OE平分∠BOC求出∠DOE的度数； (2)由(1)可得出结论∠DOE=∠AOC，从而用含a的代数式表示出∠DOE的度数； (3)①由∠COD是直角，OE平分∠BOC可得出∠COE=∠BOE=90...

    查看答案和解析>>

    同步练习册答案