
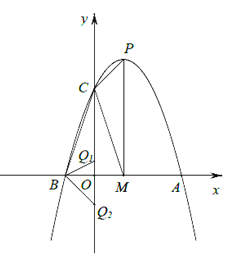
【题目】平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+3与y轴相交于点C,与x轴正半轴相交于点A,OA=OC,与x轴的另一个交点为B,对称轴是直线x=1,顶点为P.
(1)求这条抛物线的表达式和顶点P的坐标;
(2)抛物线的对称轴与x轴相交于点M,求∠PMC的正切值;
(3)点Q在y轴上,且△BCQ与△CMP相似,求点Q的坐标.

【答案】(1)(1,4)(2)(0, ![]() )或(0,-1)
)或(0,-1)
【解析】试题分析:(1)先求得点C的坐标,再由OA=OC得到点A的坐标,再根据抛物线的对称性得到点B的坐标,利用待定系数法求得解析式后再进行配方即可得到顶点坐标;
(2)由OC//PM,可得∠PMC=∠MCO,求tan∠MCO即可 ;
(3)分情况进行讨论即可得.
试题解析:(1)当x=0时,抛物线y=ax2+bx+3=3,所以点C坐标为(0,3),∴OC=3,
∵OA=OC,∴OA=3,∴A(3,0),
∵A、B关于x=1对称,∴B(-1,0),
∵A、B在抛物线y=ax2+bx+3上,
∴![]() ,∴
,∴![]() ,
,
∴抛物线解析式为:y=-x2+2x+3=-(x-1)2+4,
∴顶点P(1,4);
(2)由(1)可知P(1,4),C(0,3),所以M(1,0),∴OC=3,OM=1,
∵OC//PM,∴∠PMC=∠MCO,
∴tan∠PMC=tan∠MCO=![]() =
=![]() ;
;
(3)Q在C点的下方,∠BCQ=∠CMP,
CM=![]() ,PM=4,BC=
,PM=4,BC=![]() ,
,
∴![]() 或
或![]() ,
,
∴CQ=![]() 或4,
或4,
∴Q1(0, ![]() ),Q2(0,-1).
),Q2(0,-1).


科目:初中数学 来源: 题型:
【题目】如图,李师傅想用长为80米的栅栏,再借助教学楼的外墙围成一个矩形的活动区![]() . 已知教学楼外墙长50米,设矩形
. 已知教学楼外墙长50米,设矩形![]() 的边
的边![]() 米,面积为
米,面积为![]() 平方米.
平方米.
(1)请写出活动区面积![]() 与
与![]() 之间的关系式,并指出
之间的关系式,并指出![]() 的取值范围;
的取值范围;
(2)当![]() 为多少米时,活动区的面积最大?最大面积是多少?
为多少米时,活动区的面积最大?最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为6cm的⊙O中,点A是劣弧![]() 的中点,点D是优弧
的中点,点D是优弧![]() 上一点,且∠D=30下列四个结论:①OA⊥BC;②BC=
上一点,且∠D=30下列四个结论:①OA⊥BC;②BC=![]() cm;③cos∠AOB=
cm;③cos∠AOB=![]() ;④四边形ABOC是菱形. 其中正确结论的序号是( )
;④四边形ABOC是菱形. 其中正确结论的序号是( )

A. ①③ B. ①②③④ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
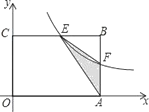
【题目】如图,在矩形OABC中,OA=6,OC=4,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数![]() 的图象与BC边交于点E.
的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校6名教师和234名学生集体外出活动,准备租用45座大车或30座小车.若租用1辆大车2辆小车共需租车费1000元;若租用2辆大车一辆小车共需租车费1100元.
(1)求大、小车每辆的租车费各是多少元?
(2)若每辆车上至少要有一名教师,且总租车费用不超过2300元,求最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个横坐标,纵坐标均为整数的点,其顺序按图中“→”方向依次排列:(1,0)(2,0)(2,1)(1,1)(1,2)(2,2)根据这个规律,第2020个点的坐标为( )
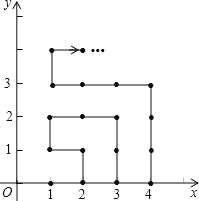
A.(45,5)B.(45,6)C.(45,7)D.(45,8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线: ![]() .
.
(1)求抛物线的顶点坐标.
(2)若直线![]() 经过(2,0)点且与
经过(2,0)点且与![]() 轴垂直,直线
轴垂直,直线![]() 经过抛物线的顶点与坐标原点,且
经过抛物线的顶点与坐标原点,且![]() 与
与![]() 的交点P在抛物线上.求抛物线的表达式.
的交点P在抛物线上.求抛物线的表达式.
(3)已知点A(0,2),点A关于![]() 轴的对称点为点B.抛物线与线段AB恰有一个公共点,结合函数图象写出
轴的对称点为点B.抛物线与线段AB恰有一个公共点,结合函数图象写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=﹣2x+4与两坐标轴分别交于点A、B,点C为线段OA上一动点,连接BC,作BC的中垂线分别交OB、AB交于点D、E.

(l)当点C与点O重合时,DE= ;
(2)当CE∥OB时,证明此时四边形BDCE为菱形;
(3)在点C的运动过程中,直接写出OD的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE=![]() AC,连接CE、OE,连接AE,交OD于点F,若AB=2,∠ABC=600,则AE的长为( )
AC,连接CE、OE,连接AE,交OD于点F,若AB=2,∠ABC=600,则AE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com