练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若，则＝______．

    【解析】设x=2k.y=3k, ∴原式=.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：贵州省遵义市桐梓县2016-2017学年七年级上学期期末考试数学试卷 题型：单选题

    下面合并同类项正确的是 ( )

    A. B.

    C. D.

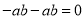    D 【解析】试题解析：3x与2x2不是同类项，不能加减，故选项A错误； 2a2b-2a2b-a2b=（2-2-1）a2b=-a2b≠1，-ab-ab=（-1-1）ab=-2ab≠0，故选项B、C均不正确； -xy2+xy2=（-1+1）xy2=0，故选项D正确． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：云南省双柏县2017-2018学年八年级上期期末数学试卷 题型：单选题

    下列说法正确的是（　　）

    A. 要了解某公司生产的100万只灯泡的使用寿命，可以采用抽样调查的方法

    B. 4位同学的数学期末成绩分别为100、95、105、110，则这四位同学数学期末成绩的中位数为100

    C. 甲乙两人各自跳远10次，若他们跳远成绩的平均数相同，甲乙跳远成绩的方差分别为0.51和0.62，则乙的表现较甲更稳定

    D. 某次抽奖活动中，中奖的概率为表示每抽奖50次就有一次中奖

    A 【解析】解：A．∵要了解灯泡的使用寿命破坏性极大，∴只能采用抽样调查的方法，故本选项正确； B．∵4位同学的数学期末成绩分别为100、95、105、110，则这四位同学数学期末成绩的中位数为102.5，故本选项错误； C．甲乙两人各自跳远10次，若他们跳远成绩的平均数相同，甲乙跳远成绩的方差分别为0.51和0.62，则甲的表现较乙更稳定，故本选项错误； D．某次抽奖活动...

    查看答案和解析>>

    科目：初中数学 来源：江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型：解答题

    已知抛物线的顶点坐标是（1，－4），且经过点（0，－3），求与该抛物线相应的二次函数表达式．

    二次函数表达式为y=(x－1)2－4或y=x2－2 x－3 【解析】试题分析：由于知道了顶点坐标是（1，－4），所以可设顶点式求解，即设y=a(x－1)2－4，然后把点（0，－3）代入即可求出系数a，从而求出解析式. 【解析】 设y=a(x－1)2－4， ∵经过点（0，－3）， ∴－3= a(0－1)2－4， 解得a=1 ∴二次函数表达式为y=(x－1)2－4...

    查看答案和解析>>

    科目：初中数学 来源：江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型：填空题

    若一个圆锥的侧面展开图是一个半径为3cm，圆心角为120°的扇形，则该圆锥的侧面面积为_____cm2（结果保留π）．

    3π 【解析】.

    查看答案和解析>>

    科目：初中数学 来源：江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型：单选题

    函数y＝3（x﹣2）2＋4的图像的顶点坐标是（ 　）

    A. （3，4） B. （﹣2，4） C. （2，4） D. （2，﹣4）

    C 【解析】函数y＝3（x﹣2）2＋4的图像的顶点坐标是（2，4）.8 故选C.

    查看答案和解析>>

    科目：初中数学 来源：山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型：解答题

    （1）计算： ；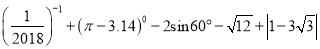

    （2）先化简，再求值： ，其中x=4﹣tan45°．

    (1)2018；（2）. 【解析】试题分析：（1）根据负整数指数幂，零指数幂的定义，特殊角的三角函数值，二次根式的性质，绝对值的意义化简计算即可； （2）先用分式的混合运算法则化简分式，然后代入求值即可． 试题解析：【解析】 （1）原式==2018； （2）原式=== 当x=4﹣tan45°=4－1=3时，原式=．

    查看答案和解析>>

    科目：初中数学 来源：山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型：单选题

    已知关于x的方程x2+3x+a=0有一个根为﹣2，则另一个根为（　　）

    A. 5 B. ﹣1 C. 2 D. ﹣5

    B 【解析】根据一元二次方程根与系数的关系，利用两根和，两根积，即可求出a的值和另一根． 【解析】 设一元二次方程的另一根为x1， 则根据一元二次方程根与系数的关系， 得﹣2+x1=﹣3， 解得：x1=﹣1． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    一般情况下，一个分式通过适当的变形，可以化为整式与分式的和的形式，例如：

    ①；

    ②

    (1)试将分式化为一个整式与一个分式的和的形式；

    (2)如果分式的值为整数，求x的整数值.

    （1）；（2）x=2或0． 【解析】试题分析：（1）原式==1－；（2）原式===+2x+2，因为分式的值为整数，且x为整数，所以x－1=±1，即x=2或0． 试题解析： （1）原式==1－； （2）原式===2（x－1）+4+=+2x+2， ∵分式的值为整数，且x为整数， ∴x－1=±1， ∴x=2或0．

    查看答案和解析>>

    同步练习册答案