
【题目】为报答当年5.12汶川地震各地的驰援深情,四川某农产品公司决定将本公司农业基地生产的蔬菜水果全部运到湖北武汉,支援武汉人民抗击新冠疫情.为了运输的方便,将蔬菜和水果分别打包成件,蔬菜和水果共260件,蔬菜比水果多40件.
(1)求打包成件的蔬菜和水果各多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批物资全部运往武汉.已知甲种货车最多可装蔬菜30件和水果13件,乙种货车最多可装蔬菜和水果各15件.如果甲种货车每辆需付运输费3000元,乙种货车每辆需付运输费2400元.则公司安排甲、乙两种货车时有几种方案?并说明公司选择哪种方案可使运输费最少?
【答案】(1)打包成件的蔬菜有150件,水果有110件;(2)4种,租用甲种货车2辆,租用乙种货车6辆,最少运费是20400元
【解析】
(1)设打包成件的蔬菜有x件,水果有y件,利用蔬菜和水果共260件,蔬菜比水果多40件可列两个方程组成方程组,然后解方程组即可;
(2)设租用甲种货车x辆,利用甲乙货车装蔬菜的数量和甲乙货车装水果的数量列不等式组,解不等式求出它的正整数解可得到运输方案,然后比较各方案的运输费即可.
解(1)设打包成件的蔬菜有x件,水果有y件,则
![]() 解得
解得![]() ,
,
答:打包成件的蔬菜有150件,水果有110件.
(2)设租用甲种货车a辆,则
![]()
解得![]()
∴设计方案分别为:
方案 | 甲车 | 乙车 | 运 费 |
① | 2 | 6 | 2×3000+6×2400=20400 |
② | 3 | 5 | 3×3000+5×2400=21000 |
③ | 4 | 4 | 4×3000+4×2400=21600 |
④ | 5 | 3 | 5×3000+3×2400=22200 |
∴方案①运费最少,最少运费是20400元.
也可以用函数方法求最值得到最少运费.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】某数学小组对函数y1=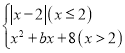 图象和性质进行探究.当x=4时,y1=0.
图象和性质进行探究.当x=4时,y1=0.
(1)当x=5时,求y1的值;
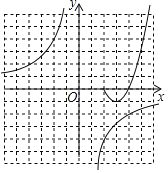
(2)在给出的平面直角坐标系中,补全这个函数的图象,并写出这个函数的一条性质;
(3)进一步探究函数图象并解决问题:已知函数y2=﹣![]() 的图象如图所示,结合函数y1的图象,直接写出不等式y1≥y2的解集.
的图象如图所示,结合函数y1的图象,直接写出不等式y1≥y2的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
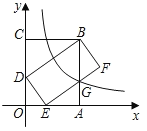
【题目】如图,矩形OABC的顶点A、C分别在x轴、y轴的正半轴上,点D在边OC上,且BD=OC,以BD为边向下作矩形BDEF,使得点E在边OA上,反比例函数y![]() (k≠0)的图象经过边EF与AB的交点G.若AG
(k≠0)的图象经过边EF与AB的交点G.若AG![]() ,DE=2,则k的值为____.
,DE=2,则k的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)直接写出抛物线的解析式为:;
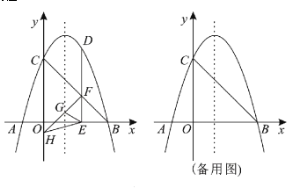
(2)点![]() 为第一象限内抛物线上的一动点,作
为第一象限内抛物线上的一动点,作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的垂线与抛物线的对称轴和
的垂线与抛物线的对称轴和![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①求![]() 的最大值;
的最大值;
②连接![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 铀交于
铀交于![]() ,与
,与![]() 轴交于
轴交于![]() 抛物线的顶点为
抛物线的顶点为![]() 直线
直线![]() 过
过![]() 交
交![]() 轴于
轴于![]() .
.
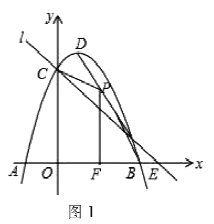
(1)写出![]() 的坐标和直线
的坐标和直线![]() 的解析式;
的解析式;
(2)![]() 是线段
是线段![]() 上的动点(不与
上的动点(不与![]() 重合),
重合),![]() 轴于
轴于![]() 设四边形
设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的两数关系式,并求
之间的两数关系式,并求![]() 的最大值;
的最大值;
(3)点![]() 在
在![]() 轴的正半轴上运动,过
轴的正半轴上运动,过![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于
于![]() 交抛物线于
交抛物线于![]() 连接
连接![]() ,将
,将![]() 沿
沿![]() 翻转,
翻转,![]() 的对应点为
的对应点为![]() .在图2中探究:是否存在点
.在图2中探究:是否存在点![]() ;使得
;使得![]() 恰好落在
恰好落在![]() 轴?若存在,请求出
轴?若存在,请求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
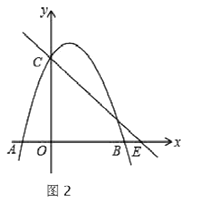
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人类的血型一般可分为A,B,AB,O型四种,宁波市中心血战2015年共有8万人无偿献血,血战统计人员由电脑随机选出20人,血型分别是:
O,A,O,B,O,A,A,AB,A,O,O,B,AB,B,O,A,O,B,O,A.
(1)请设计统计表分类统计这20人各类血型人数;
(2)若每位献血者平均献血200毫升,一年中宁波市各医院O型血用血量约为6×106毫米,请你估计2015年这8万人所献的O型血是否够用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,点E在BC边上,且CA=CE,过A,C,E三点的⊙O交AB于另一点F,作直径AD,连结DE并延长交AB于点G,连结CD,CF.
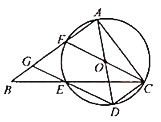
(1)求证:四边形DCFG是平行四边形;(2)当BE=4,CD=![]() AB时,求⊙O的直径长.
AB时,求⊙O的直径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=∠B=30°,过点C作CD⊥AC,交AB于点D.
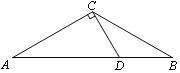
(1)作⊙O,使⊙O经过A、C、D三点(尺规作图,保留作图痕迹,不写作法);
(2)判断直线 BC与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 的顶点是A(1,3),将OA绕点O逆时针旋转
的顶点是A(1,3),将OA绕点O逆时针旋转![]() 后得到OB,点B恰好在抛物线上,OB与抛物线的对称轴交于点C.
后得到OB,点B恰好在抛物线上,OB与抛物线的对称轴交于点C.

(1)求抛物线的解析式;
(2)P是线段AC上一动点,且不与点A,C重合,过点P作平行于x轴的直线,与![]() 的边分别交于M,N两点,将
的边分别交于M,N两点,将![]() 以直线MN为对称轴翻折,得到
以直线MN为对称轴翻折,得到![]() .
.
设点P的纵坐标为m.
①当![]() 在
在![]() 内部时,求m的取值范围;
内部时,求m的取值范围;
②是否存在点P,使![]() ,若存在,求出满足m的值;若不存在,请说明理由.
,若存在,求出满足m的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com