
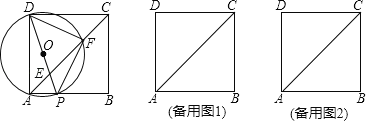
【题目】如图,在正方形ABCD中,AB=4,动点P从点A出发,以每秒2个单位的速度,沿线段AB方向匀速运动,到达点B停止.连接DP交AC于点E,以DP为直径作⊙O交AC于点F,连接DF、PF.
(1)求证:△DPF为等腰直角三角形;
(2)若点P的运动时间t秒.
①当t为何值时,点E恰好为AC的一个三等分点;
②将△EFP沿PF翻折,得到△QFP,当点Q恰好落在BC上时,求t的值.
【答案】(1)详见解析;(2)①1;②![]() ﹣1.
﹣1.
【解析】
(1)要证明三角形△DPF为等腰直角三角形,只要证明∠DFP=90°,∠DPF=∠PDF=45°即可,根据直径所对的圆周角是90°和同弧所对的圆周角相等,可以证明∠DFP=90°,∠DPF=∠PDF=45°,从而可以证明结论成立;
(2)①根据题意,可知分两种情况,然后利用分类讨论的方法,分别计算出相应的t的值即可,注意点P从A出发到B停止,t≤4÷2=2;
②根据题意,画出相应的图形,然后利用三角形相似,勾股定理,即可求得t的值.
证明:(1)∵四边形ABCD是正方形,AC是对角线,
∴∠DAC=45°,
∵在⊙O中,![]() 所对的圆周角是∠DAF和∠DPF,
所对的圆周角是∠DAF和∠DPF,
∴∠DAF=∠DPF,
∴∠DPF=45°,
又∵DP是⊙O的直径,
∴∠DFP=90°,
∴∠FDP=∠DPF=45°,
∴△DFP是等腰直角三角形;
(2)①当AE:EC=1:2时,
∵AB∥CD,
∴∠DCE=∠PAE,∠CDE=∠APE,
∴△DCE∽△PAE,
∴![]() ,
,
∴![]() ,
,
解得,t=1;
当AE:EC=2:1时,
∵AB∥CD,
∴∠DCE=∠PAE,∠CDE=∠APE,
∴△DCE∽△PAE,
∴![]() ,
,
∴![]() ,
,
解得,t=4,
∵点P从点A到B,t的最大值是4÷2=2,
∴当t=4时不合题意,舍去;
由上可得,当t为1时,点E恰好为AC的一个三等分点;
②如右图所示,
∵∠DPF=90°,∠DPF=∠OPF,
∴∠OPF=90°,
∴∠DPA+∠QPB=90°,
∵∠DPA+∠PDA=90°,
∴∠PDA=∠QPB,
∵点Q落在BC上,
∴∠DAP=∠B=90°,
∴△DAP∽△PBQ,
∴![]() ,
,
∵DA=AB=4,AP=2t,∠DAP=90°,
∴DP=![]() =2
=2![]() ,PB=4﹣2t,
,PB=4﹣2t,
设PQ=a,则PE=a,DE=DP﹣a=2![]() ﹣a,
﹣a,
∵△AEP∽△CED,
∴![]() ,
,
即![]() ,
,
解得,a=![]() ,
,
∴PQ=![]() ,
,
∴ ,
,
解得,t1=﹣![]() ﹣1(舍去),t2=
﹣1(舍去),t2=![]() ﹣1,
﹣1,
即t的值是![]() ﹣1.
﹣1.



科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
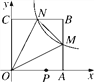
A. 6![]() B. 10 C. 2
B. 10 C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数
,1)在反比例函数![]() 的图象上.
的图象上.
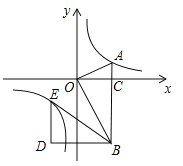
(1)求反比例函数![]() 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP=![]() S△AOB,求点P的坐标;
S△AOB,求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2020比佛利”无锡马拉松赛将于3月22日鸣枪开跑,本次比赛设三个项目:A.全程马拉松;B.半程马拉松;C.迷你马拉松.小明和小红都报名参与该赛事的志愿者服务工作,若两人都已被选中,届时组委会随机将他们分配到三个项目组.
(1)小明被分配到“迷你马拉松”项目组的概率为 ;
(2)请利用树状图或列表法求两人被分配到同一个项目组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
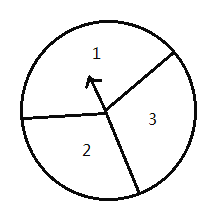
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.
(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为 ;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,双曲线y=![]() (k≠0)与直线y=ax+b(a≠0)交于A,B两点,直线AB分别交x轴,y轴于C、D两点,若OA=OC,A点坐标为(4,3).
(k≠0)与直线y=ax+b(a≠0)交于A,B两点,直线AB分别交x轴,y轴于C、D两点,若OA=OC,A点坐标为(4,3).

(1)分别求出双曲线与直线的函数表达式;
(2)若P为双曲线上一点,且横坐标为2,H为直线AB上一点,且PH+![]() HC最小,延长PH交x轴于点E,将线段OE沿x轴平移得线段O'E',在平移过程中,是否存在某个位置使|BO'﹣AE'|的值最大值,求出最大值并求出此时E点坐标.
HC最小,延长PH交x轴于点E,将线段OE沿x轴平移得线段O'E',在平移过程中,是否存在某个位置使|BO'﹣AE'|的值最大值,求出最大值并求出此时E点坐标.
(3)在(2)的情况下,将直线OA沿线段CE平移,平移过程中交y=![]() (x>0)的图象于M(M与点A不重合)交x轴于点N,在平面内找一点G,使M、N,E,G为顶点的四边形为矩形?直接写出G的坐标.
(x>0)的图象于M(M与点A不重合)交x轴于点N,在平面内找一点G,使M、N,E,G为顶点的四边形为矩形?直接写出G的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com